Лекція №5 Взаємне положення точки, прямої і площини у просторі. Інцидентність, паралельність, перпендикулярність прямої та площини, двох площин

5.1. Умови взаємної інцидентност і, паралельності та перпендикулярності як параметри.

Точка, пряма та площина попарно можуть бути інцидентними, паралельними або взаємно перпендикулярними. Ці три умови еквівалентні заданню певного числа параметрів. Тому, визначаючи загальне число параметрів для комбінацій даного виду, слід враховувати розмірність конкретної умови.

Інцидентність. Інцидентність точки прямій на площині еквівалентна одному параметру, тому для задання такої точки досить одного параметра (наприклад, відстані від точки відліку). Інцидентність точки прямій, розміщеній у просторі, еквівалентна двом параметрам. Отже, для задання точки залишається вільним один параметр, тому досить задати, наприклад, її абсцису, а за допомогою вертикальної лінії сполучення визначити ординату та аплікату точки.

Інцидентність точки площині еквівалентна заданню одного параметра, тому для задання точки на площині залишаються вільними два параметри, які можна реалізувати, наприклад, заданням фронтальної чи горизонтальної проекції точки (рис. 5.1).

Інцидентність прямої площині еквівалентна заданню двох параметрів, а оскільки прямих у просторі ~4, то вільними залишаються два параметри, за допомогою яких задається фронтальна чи горизонтальна проекція прямої.

Паралельність. Можливі три випадки паралельності: двох прямих; прямої та площини; двох площин.

Паралельність двох прямих на площині еквівалентна заданню одного параметра. Тому для зображення прямої Ь, паралельної прямій а, досить одного параметра (рис. 5.2).

Паралельність двох прямих у просторі еквівалентна заданню двох параметрів (рис. 5.3, а). Справді, всього прямих у просторі є ~4, а прямих, паралельних даній, є ~2 (за кількістю точок площини П, через кожну з яких можна провести пряму, паралельну даній). Таким чином, паралельність двох прямих у просторі еквівалентна заданню двох параметрів, тому для побудови прямої Ь, паралельної даній а, досить двох параметрів (рис. 5.3, б).

Паралельність прямої та площини еквівалентна заданню одного параметра. Справді, всього прямих в просторі є ~4, а прямих, паралельних площині, — ~3. Отже, для задання прямої, паралельної площині, потрібні три параметри. Нарис. 5.4 показано побудову прямої паралельної площині. У площині П2 двома параметрами задано довільну точку О, через яку проведено пряму т, паралельну будь-якій прямій площини (у даному випадку паралельну АС), — ще один параметр.

Паралельність двох площин еквівалентна заданню двох параметрів. Отже, для задання площини, паралельної даній, досить одного параметра (рис. 5.5). На рисунку площину Л задано слідами. Для побудови площини Ф, що паралельна їй, досить на осі абсцис задати точку і провести через неї сліди площини, паралельно заданим.

Перпендикулярність. Можливі три випадки перпендикулярності: двох прямих;

Прямої та площини; двох площин.

Перпендикулярність двох прямих, що лежать у площині, еквівалентна заданню одного параметра. Отже, щоб побудувати пряму Ь, перпендикулярну до даної прямої а, досить одного параметра.

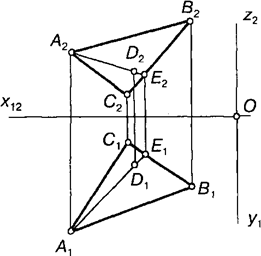
Рис. 5.1.

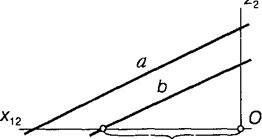
Рис. 5.2.

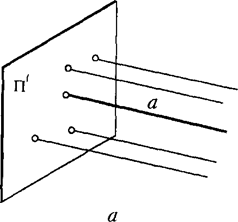
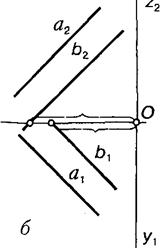
Рис. 5.3.

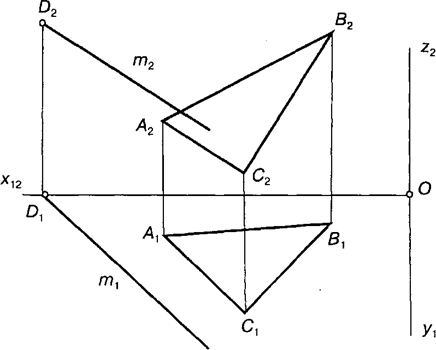
Рис. 5.4.

У просторi перпеНдикулярнiсть двох прямих еквiвалентна теж заданию одного параметра. Справдi, всього прямих в просторi є ~4, а прямих, перпендикулярних до даної, . Тому, щоб побудувати пряму, перпендикулярну до прямы, мимобiжної з нею, слiд мати три параметри, а для побудови прямої, перпендикулярної до прямї, яка перетинає i, досить двох параметрiв. На рис. 5.7, а побудовано пряму, перпендикулярну до даної, i таку, що перетинає й. На рис. 5.7, 6 побудовано пряму, перпендикулярну до мимобiжної з нею прямої. У першому випадку використано один параметр, а в другому — два. достатнiсть одного (двох) параметра пояснюсться тим, що одна з прямих паралельна площинi проекцiй.

Перпендикулярнiсть прямої та площини. Всього прямих у просторi є ~4, а прямих, що задовольняють умову перпендикулярностi до площини,

~2 (за кiлькiстю точок у площинi). Таким чином, умова перпендикулярностi прямої до площини еквiвалентна заданию двох параметрiв. для задания прямої, перпендикулярної до площини, потрiбно два параметри, що залишились (рис. 5.8, а).У площинi, заданiй слiдами, взято фронтальну проекцiю точки А (за якою визначають горизонтальну проекцiю). Пiсля цього ставлять перпендикуляр n.

Перпендикулярнiсть двох площин. Всього площин у просторi є ~3, а площин, перпендикулярних до даної, — ~2 (вiдповiдно до кiлькостi прямих, що належать площинi). Отже, перпендикулярнiсть двох площин еквiвалентна заданню одного параметра. для задання площини, перпендикулярної до даної, потрiбнi два параметри, що залишилися. Оскiльки площина, перпендикулярна до даної, мiстить перпендикуляр до неї, то на осi х12 одним параметром задають точку А12. Проводять з неї перпендикуляр до площини П i знаходять i його основу М. Задаючи в площинi Г ще одну точку N (другий параметр), визначають пряму NМ, яка разом з n задас перпендикулярну площину (рис. 5.8, 6).

У табл. 5.1 подано деякi геометричнi умови та еквiвалентнi iм параметри у двота тривимiрному просторах.

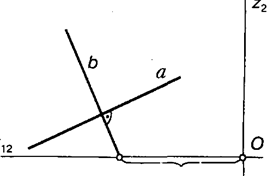
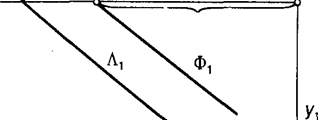
Рис. 5.5. Рис. 5.6.

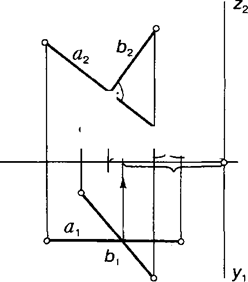
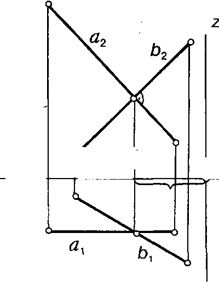
Рис. 5.7.

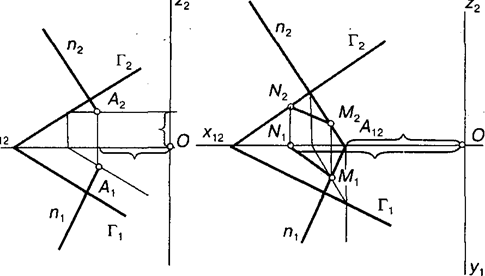
а б

Рис. 5.8.

Таблиця 5.1. Геометричні умови та еквівалентні їм параметри.

Таблиця 5.2. Дані для побудови проекції піраміди.

Список рекомендованої літератури

Гордон В. О., Семенцов-Огиевский М. А. Курс начертательной геометрии.- М.: Изд-во Наука, 1988. – 270 с.

Михайленко В. Є., Ковальов С. М. та ін. Нарисна геометрія. Підручник для вузів. – К.:Вища школа,1993. – 134с.

Винницкий И. Г. Начертательная геометрия. Учебник для вузов. – М.: Высшая школа, 1985.- 168с.

Михайленко В. Е. та ін. Инженерная графика. – Киев: Высшая школа, 1990.-290 с.

Михайленко В. Е. та ін. Інженерна та комп’ютерна графіка. За ред. Михайленка В. Е. Київ: Вища школа, 2000.