Динамикой называется раздел ТМ, в которой изучается механическое движение материальной точки, системы материальных точек и абсолютного твердого тела с учет сил, действующих сил, действующих на эти движущиеся объекты.
Первая задача динамики — заключается в том, что по заданному механическому движению тела определяют силы, под действием которых совершается это движение.
Вторая задача состоит в том, что по заданным силам, приложенным к телу, и начальным условиям определяют движение, которое они вызывают.
Динамику разделяют на динамику материальной точки, динамику системы материальных точек и динамику твердого тела.
Законы Ньютона.
В основе динамики лежат законы И. Ньютона, изложены им в «Математических началах натуральной философии» (1687).
Системы координат, в которых справедливы законы Ньютона, называются инерциальными.
1-ый закон Ньютона.
Изолированная материальная точка движется равномерно и прямолинейно либо находится в состоянии покоя до тех пор, пока действие других тел на эту материальную точку не изменит это состояние.
Изолированной называется материальная точка, взаимодействием которой с окружающими телами пренебрегают.
Из закона инерции следует, что самопроизвольное изменение движения точки невозможно.
2-ой закон Ньютона.
Скорость изменения количества движения материальной точки равна силе, действующей на эту точку.
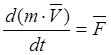
— количество движения материальной точки;
— масса точки.
При движении с большими скоростями масса будет равна (формула Лоренца):
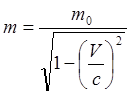
— масса покоящегося объекта;
— скорость движения.
При 
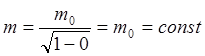
Тогда можно записать:
Отсюда: ускорение материальной точки пропорционально приложенной к ней силе и имеет одинаковое направление.
Массой материальной точки называется физическая величина, являющаяся мерой её инертных и гравитационных свойств.
3-ий закон Ньютона.
Силы взаимодействия двух материальных точек или двух тел равны по величине, направлены в противоположные стороны и имеют общую линию действия.
Дифференциальные уравнения движения материальной точки.
Установим дифференциальные уравнения движения материально точки. Если движение задано в векторной форме с помощью радиус-вектора 
, то:
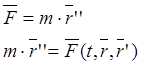
в координатной форме:
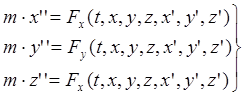Динамические уравнения движения материальной точки
Где 
— координаты;
— проекции ускорений;
— проекции скоростей.
Две основные задачи динамики материальной точки.
Первая: определить равнодействующую сил 
, действующих на материальную точку, если заданы её масса и кинематические уравнения движения.
Движение материальной точки массой задано уравнениями:
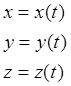
Дифференцируя эти уравнения, получаем:
Тогда:
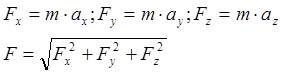
Вторая: определит кинематические уравнения движения материальной точки, если заданы её масса , приложенная к ней сила и начальные условия движения.
Решение этой задачи сводится к интегрированию дифференциальных уравнений движения материальной точки.
Сначала находят проекции силы на оси координат и затем интегрируют. Получают:
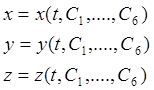
Для решения этой системы используют начальные условия и знания о том, что:
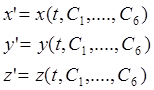
Определяют постоянные интегрирования и получают уравнения движения:
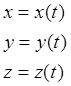
Решение второй задачи динамики включает следующие операции:
Составление динамических уравнений движения материальной точки в соответствии с условиями задачи;
Интегрирование дифференциальных уравнений;
Определение значений постоянных интегрирования;
Нахождение закона движения.
Уравнение движения несвободной материальной точки:
Где — активные силы;
— реакции связи.
Если спроецировать на координатные оси, то получим:
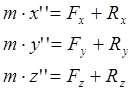
Основные теоремы динамики.
Нужно записать Определения.
Системой материальных точек называется совокупность материальных точек, положения и движения которых взаимосвязаны. Различают свободные и несвободные системы.
Массой системы, состоящей из 
материальных точек, называется сумма масс точек системы:
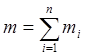
Центром масс системы материальных точек называется центр параллельных сил 
, сообщающих движение точкам системы с одинаковым ускорением или поступательное движение. Координаты центра масс:
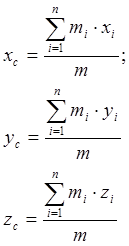
Теорема о движении центра масс:
Центр масс системы материальных точек движется как свободная материальная точка, масса которой равна массе всей системы и на которую действуют сила, равная главному вектору внешних сил.
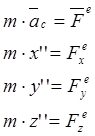
Количество движения системы материальных точек называется вектор, равный произведению массы точек на вектор её скорости:
Количество движения системы материальных точек (твердого тела) равно произведению массы системы (твердого тела) на скорость её (его) центра масс:
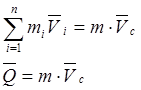
Теорема об изменяющем количестве движения системы материальных точек.
В дифференциальной форме:
Производная по времени от количества движения системы материальных точек равно главному вектору внешних сил, действующих на систему:
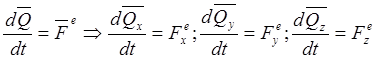
Следствия.
Одними внутренними силами нельзя изменить количество движения системы;
Если главный вектор внешних сил, действующих на систему, равен нулю, то количество движения материальной системы остается постоянным;
Если проекция главного вектора внешних сил, приложенных к системе на некоторую неподвижную в инерциальной системе координат ось, равна нулю, то проекция количества движения на эту ось остается постоянной.
2 и 3 следствия — это законы сохранения количества движения материальной системы.
В интегральной форме:
Изменения количества движения системы материальных точек за некоторый промежуток времени 
равно полному импульсу главного вектора внешних сил, приложенных к точкам системы, за тот же промежуток времени.
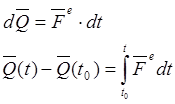
— элементарный импульс.
Полный импульс:
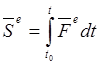
Кинетическая энергия. Работа.
Энергией называется физическая величина, которая является скалярной мерой движения материи при переходе от одной формы движения в другую (например, механической в тепловую).
[Дж]
Е — полная энергия;
Т — кинетическая;
П — потенциальная.
Кинетической энергией материальной точки называется скалярная мера механического движения, равная половине произведения массы точки на квадрат её скорости:
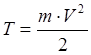
Кинетическая энергия поступательно движущегося тела:
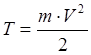
Кинетическая энергия тела, вращающегося вокруг неподвижной точки:
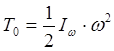
— осевой момент инерции
Вокруг оси:
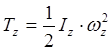
При плоском движении:
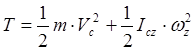
Теорема об изменении КЭ материальной точки:
Приращение кинетической энергии материальной точки на некотором отрезке дуги её траектории равно работе силы, приложенной к точке на этом же отрезке дуги траектории.
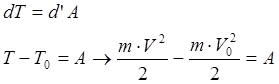
Элементарная работа силы представляет собой скалярную меру действия силы, равную скалярному произведению силы на элементарное перемещение точки её приложения.
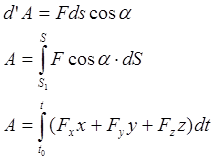
[Вт] – мощность это физическая величина, характеризующая быстроту выполнения работы силой, приложенной к материальной точке, и равна скалярному произведению силы на скорость точки.
Частные случаи:
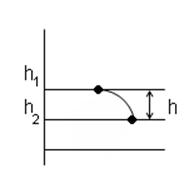
Работа силы тяжести не зависит от формы траектории движущейся материальной точки, а зависит от крайних её положений:
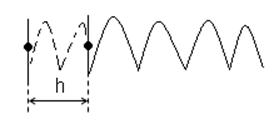
Работа силы упругости зависит от крайних положений точки.
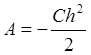
Принцип д’Аламбера.
Пусть на материальную точку действует активная сила И реакция связи . Для несвободной точки:
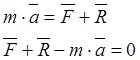
— д’Аламберова сила инерции.
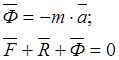
Принцип: в случае несвободной материальной точки в каждый момент времени сумма активных сил, приложенных к тоске, реакций связей и сил инерции равна нулю.
Сила инерции 
всегда направлена в сторону, противоположную ускорению 
.