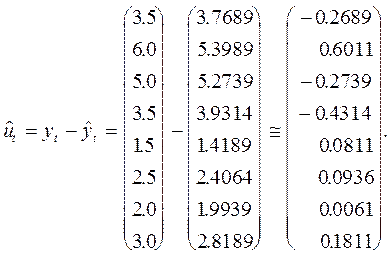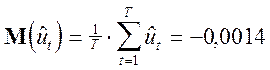Как уже ранее было отмечено, наблюдаемая случайная переменная ![]() , которую называют Регрессандом, может быть представлена линейной функцией от
, которую называют Регрессандом, может быть представлена линейной функцией от ![]() наблюдаемых переменных
наблюдаемых переменных ![]() , называемых Регрессорами, и от скрытых (латентных) случайных переменных
, называемых Регрессорами, и от скрытых (латентных) случайных переменных ![]() , называемых Случайными возмущениями
, называемых Случайными возмущениями
![]()
Функция называется регрессионной[1]. Имеющийся ряд наблюдений по ![]() позволяет для каждого наблюдения получить соотношение
позволяет для каждого наблюдения получить соотношение
![]() (I. 1)
(I. 1)
Вероятностный характер возмущений делает регрессионную функцию стохастической.
Ряды данных (наблюдений) длиной ![]() для регрессанда и каждого из регрессоров необходимы для того, чтобы оценить параметры модели статистически. Количество рядов равно
для регрессанда и каждого из регрессоров необходимы для того, чтобы оценить параметры модели статистически. Количество рядов равно ![]() в каждом
в каждом ![]() точек наблюдения[2]:
точек наблюдения[2]:
![]()
Длина временных рядов ![]() образует так называемый опорный Базовый период оценки.
образует так называемый опорный Базовый период оценки.
Таким образом, для каждого из наблюдений имеем следующие соотношения:
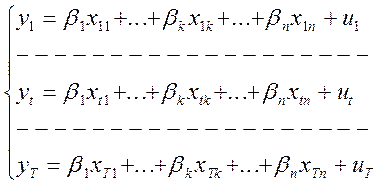 .
.
Обозначая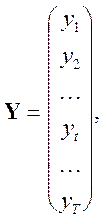
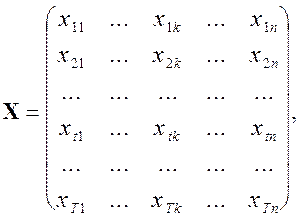
![]() Мерный
Мерный ![]() Мерная матрица
Мерная матрица
вектор
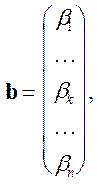
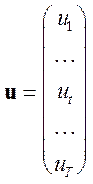 ,
,
![]() Мерный
Мерный ![]() Мерный
Мерный
вектор вектор
Выше приведенное соотношение можно переписать в векторной форме: ![]() Матрицу вида
Матрицу вида ![]() будем называть матрицей данных.
будем называть матрицей данных.
При формировании матрицы данных, значения измеряемых величин “шкалируются” относительно фиксированных значений одного из регрессоров (например, первого).
ПРИМЕР: Пусть для простой линейной регрессии
![]()
Имеются два следующих ряда данных длиной ![]()
|
|
|
|
Матрица данных |
|
1 2 3 4 5 6 |
2 3 3 4 4 5 |
1 1 3 3 5 5 |
|
Выражение вида ![]() называют Систематической частью регрессанда.
называют Систематической частью регрессанда.
I. 1 Одношаговый метод наименьших квадратов построения модели множественной регрессии.
Вернемся к рассмотрению уравнения (I. 1). Применим к обеим частям этого уравнения оператор математического ожидания. Тогда получим[3]
![]()
Эту величину можно прогнозировать с помощью регрессионного уравнения.
Очевидно, что на момент постановки экспериментов по выявлению зависимости между переменными величинами ![]() и
и ![]() , точные значения параметров
, точные значения параметров ![]() неизвестны. Они могут быть только оценены. Основной принцип оценки параметров регрессионной модели является Принцип минимума суммы квадратов ошибок (отклонений).
неизвестны. Они могут быть только оценены. Основной принцип оценки параметров регрессионной модели является Принцип минимума суммы квадратов ошибок (отклонений).
Важный этап — Формирование целевой функции.
Ошибка или отклонение: ![]()
Квадрат ошибки: ![]()
Здесь ![]() Значения параметров, получаемые в результате оценок.
Значения параметров, получаемые в результате оценок.
Сумма квадратов ошибок:
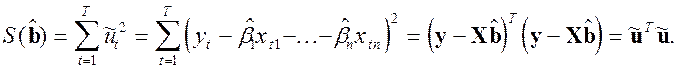
Функция ![]() при оценке регрессионных коэффициентов методом наименьших квадратов и является целевой функцией. Перепишем ее в следующем виде:
при оценке регрессионных коэффициентов методом наименьших квадратов и является целевой функцией. Перепишем ее в следующем виде:
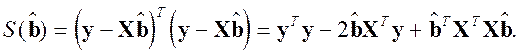
Далее, вычислим частную производную
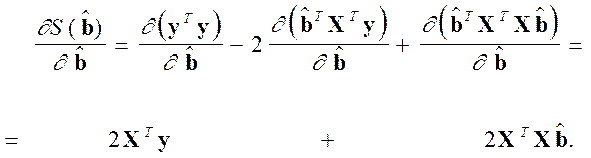
![]() Мерный вектор
Мерный вектор ![]() Мерный вектор
Мерный вектор
Необходимое условие экстремума:
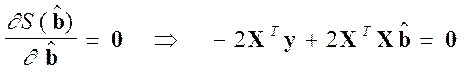
Или ![]()
В развернутом виде:
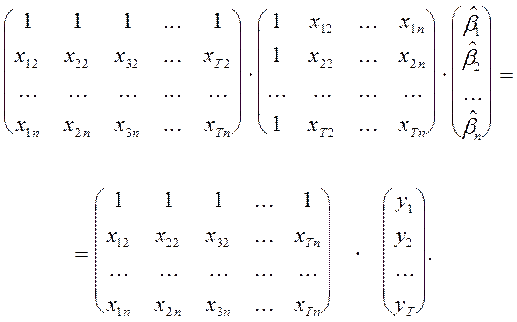
Здесь неизвестным (искомым) является вектор ![]() . В матричной записи имеем:
. В матричной записи имеем:
![]()
Подставляя найденные значения ![]() в оцениваемое регрессионное уравнение, получим так называемую Эмпирическую регрессионную функцию:
в оцениваемое регрессионное уравнение, получим так называемую Эмпирическую регрессионную функцию:
![]() (*)
(*)
Эмпирический регрессионный коэффициент ![]() в выражении (*) является частной производной эмпирической функции регрессии по
в выражении (*) является частной производной эмпирической функции регрессии по ![]() Му регрессору.
Му регрессору.
|
Таким образом: Изменение величины |
ПРИМЕР: В качестве иллюстрации, рассмотрим бюджетное обследование восьми случайно выбранных семей, которое дало следующие результаты в масштабе единиц общего выделенного признака ![]() (см. таблицу 1):
(см. таблицу 1):
Таблица 1.
|
Семья |
Накопления |
Доход |
Имущество |
|
1 |
3.5 |
45 |
60 |
|
2 |
6.0 |
55 |
36 |
|
3 |
5.0 |
50 |
36 |
|
4 |
3.5 |
40 |
55 |
|
5 |
1.5 |
20 |
90 |
|
6 |
2.5 |
25 |
75 |
|
7 |
2.0 |
20 |
80 |
|
8 |
3.0 |
30 |
70 |
Составим вспомогательную таблицу для расчетов (см. таблицу 2.):
Таблица 2.
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 3 4 5 6 7 8 |
3,5 6,0 5,0 3,5 1,5 2,5 2,0 3,0 |
1 1 1 1 1 1 1 1 |
45 55 50 40 20 25 20 30 |
60 36 36 55 90 75 80 70 |
12,25 36,00 25,00 12,25 2,25 6,25 4,00 9,00 |
2025 3025 2500 1600 400 625 400 900 |
3600 1296 1296 3025 8100 5625 6400 4900 |
2700 1980 1800 2200 1800 1875 1600 2100 |
157,5 330,0 250,0 140,0 30,0 62,5 40,0 90,0 |
210,0 216,0 180,0 192,5 135,0 187,5 160,0 210,0 |
|
å |
27 |
8 |
285 |
502 |
107 |
11475 |
34242 |
16055 |
1100 |
1491 |
|
Сред-нее |
3,375 |
1 |
35,625 |
62,75 |
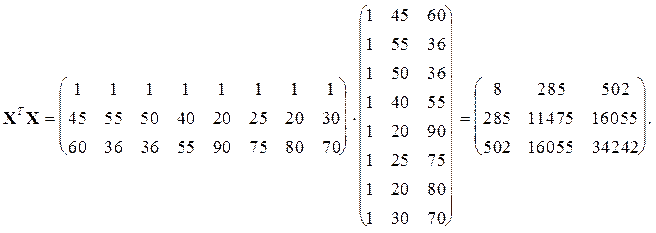
![]()
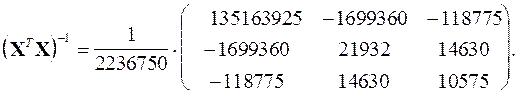
Для контроля точности, необходимо исходную матрицу ![]() умножить на
умножить на ![]() . В результате получается единичная матрица.
. В результате получается единичная матрица.
Определим вектор правой части системы нормальных уравнений
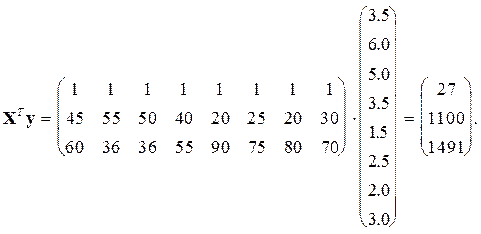
Далее, рассчитываем вектор регрессионных коэффициентов, оцененных методом 1МНК[4]:
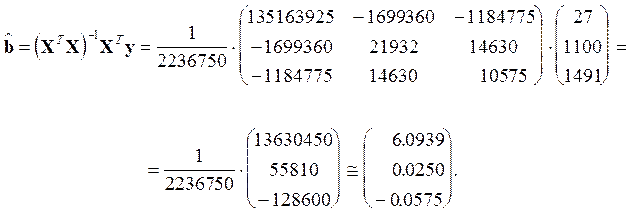
Таким образом, эмпирическая линейная функция двухфакторной регрессии примет следующий вид:
![]()
Она приводит к следующим прогнозным (расчетным) значениям регрессанда:
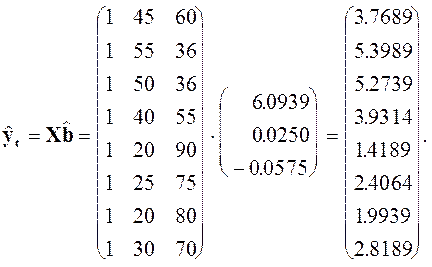
Тогда можно рассчитать вектор ошибок
|
|
Здесь величина математического ожидания ошибок:
Свидетельствует о том, что расчеты выполнены верно. В принципе, на основании одной из основных предпосылок математической модели регрессии, для точных расчетов (без округлений): |
I. 2. Стандартизированные коэффициенты регрессии.
Оцененное значение стандартизированных коэффициентов регрессии можно вычислить по следующей формуле:
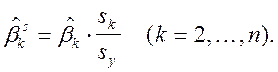
![]() Эмпирическое стандартное отклонение
Эмпирическое стандартное отклонение ![]() Го регрессора
Го регрессора ![]() ;
;
![]() Эмпирическое стандартное отклонение регрессанда.
Эмпирическое стандартное отклонение регрессанда.
|
Эмпирический стандартизированный коэффициент регрессии |
I. 3. Коэффициенты эластичности.
При интерпретации регрессионных коэффициентов необходимо принимать во внимание единицы измерения регрессанда и регрессоров. Для определения степени влияния регрессора на регрессанд без учета единиц их измерения можно вычислить коэффициент эластичности.
Эластичность регрессанда ![]() относительно регрессора
относительно регрессора ![]() :
:
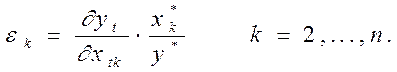
Где ![]() и
и ![]() Некоторая точка регрессионной функции.
Некоторая точка регрессионной функции.
В линейном уравнении
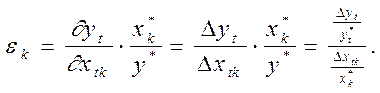
В силу того, что
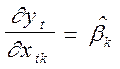
Будем иметь

Это основная формула для линейной модели.
|
Интерпретация: Если при прочих равных условиях |
I. 4. Истинная ковариационная матрица для ![]() .
.
Оценки ![]() носят стохастический характер, однако, при этом не исключается вариант наличия объективных взаимосвязей между ними.
носят стохастический характер, однако, при этом не исключается вариант наличия объективных взаимосвязей между ними.
Взаимосвязь случайных величин может проявляться в том, что условный закон распределения одной случайной величины изменяется в зависимости от значений, принимаемых другой случайной величиной. Одной из характеристик стохастической взаимосвязи двух случайных величин является Ковариация случайных величин. Напомним известное из курса теории вероятностей и математической статистики определение ковариации: Ковариацией случайных величин ![]() и
и ![]() называется число
называется число ![]() равное математическому ожиданию произведения отклонений случайных величин
равное математическому ожиданию произведения отклонений случайных величин ![]() и
и ![]() от своих математических ожиданий:
от своих математических ожиданий:
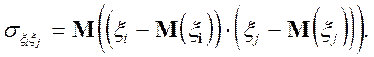
Таким образом, для характеристики оценок ![]() дисперсии
дисперсии ![]() и ковариации
и ковариации ![]() , которые можно объединить в виде матрицы:
, которые можно объединить в виде матрицы:
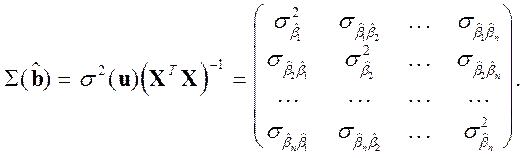
Она неизвестна и может быть лишь оценена.
Оцененная матрица: ![]() , где
, где 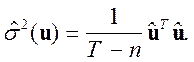
Вернемся к рассмотренному нами ранее примеру.
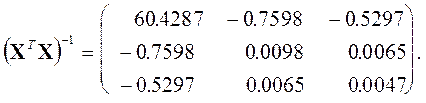
Величину ![]() можно рассчитать следующим образом:
можно рассчитать следующим образом:
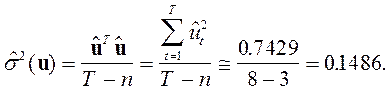
Тогда:
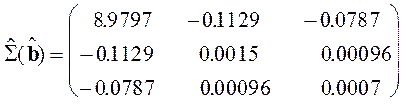
![]()
Видно, что ![]() на три-четыре прядка отличается от
на три-четыре прядка отличается от ![]() и
и ![]() . Можно сделать вывод, что оценка
. Можно сделать вывод, что оценка ![]() относительно неточна (велик разброс).
относительно неточна (велик разброс).
![]()
![]()
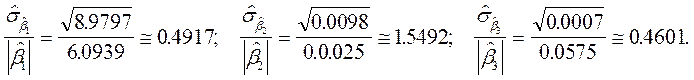
Оцененная ковариация ![]() . Следовательно, увеличение оценки
. Следовательно, увеличение оценки ![]() приводит к уменьшению оценки
приводит к уменьшению оценки ![]() . Аналогично, оцененная ковариация
. Аналогично, оцененная ковариация ![]() и увеличение оценки
и увеличение оценки ![]() приводит к уменьшению оценки
приводит к уменьшению оценки ![]() . А вот оцененная ковариация
. А вот оцененная ковариация ![]() . Следовательно изменение оценки параметра
. Следовательно изменение оценки параметра ![]() находится в прямой зависимости по отношению к изменению параметра
находится в прямой зависимости по отношению к изменению параметра ![]() .
.
К более конкретному заключению о степени связи между оцененными параметрами можно прийти, если рассчитать соответствующие коэффициенты корреляции
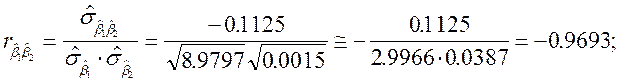
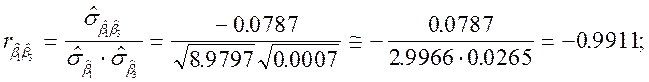
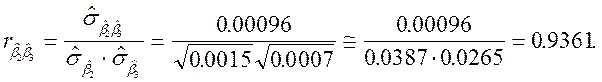
Таким образом между этими параметрами существует достаточно сильная отрицательная связь.
I. 5. Коэффициент детерминации.
Коэффициент детерминации ![]() Используется для оценки адекватности эмпирической регрессионной функции.
Используется для оценки адекватности эмпирической регрессионной функции.
Существует три различных, сводящихся друг к другу определения этого коэффициента.
Определение I.
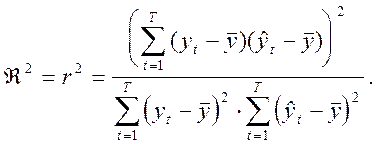
Определение II.
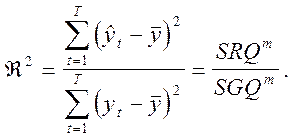
Определение III.
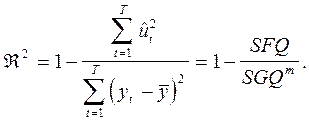
Из определения I следует, что ![]()
|
Коэффициент детерминации |
Таким образом, регрессионное уравнение оценено тем лучше, чем больше, при прочих равных условиях, коэффициент детерминации ![]() .
.
I. 6. Простейшие приемы вычисления коэффициента детерминации.
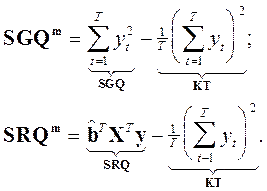
В рассмотренном выше примере с регрессорами ![]() и
и ![]() имеем
имеем
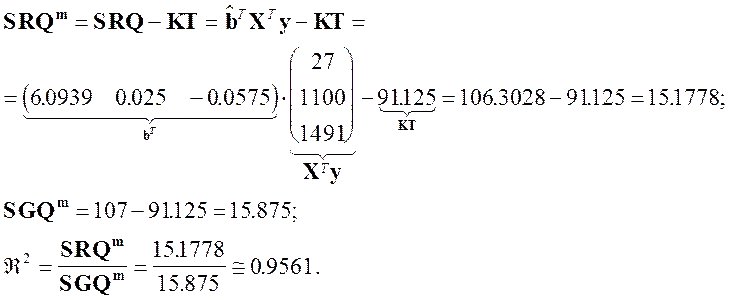
При этом использовано значение ![]() , значение которого можно получить следующим образом
, значение которого можно получить следующим образом
![]()
Рассчитайте самостоятельно коэффициент детерминации той же математической модели (регрессионной функции), оставляя только два регрессора, например, ![]() и
и ![]() .
.
Замечание: Если включить в регрессию с ![]() регрессорами дополнительный регрессор, то всегда выполняется соотношение:
регрессорами дополнительный регрессор, то всегда выполняется соотношение:
![]() С
С ![]() регрессором
регрессором![]()
![]() С
С ![]() регрессорами
регрессорами![]() .
.
Это означает, что приращение ![]() От ввода дополнительного регрессора есть величина неотрицательная.
От ввода дополнительного регрессора есть величина неотрицательная.
I. 7. Некоторые общие сведения о частном коэффициенте детерминации.
Частный коэффициент детерминации ![]() — это Предельный (граничный) вклад
— это Предельный (граничный) вклад ![]() Го регрессора в
Го регрессора в ![]() . Он показывает, на какую величину Уменьшается Коэффициент детерминации, если
. Он показывает, на какую величину Уменьшается Коэффициент детерминации, если ![]() Й регрессор (и только он!) будет исключен из группы
Й регрессор (и только он!) будет исключен из группы ![]() регрессоров.
регрессоров.
Таким образом:
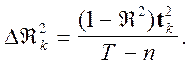
Здесь:
![]() Коэффициент детерминации, который получается при включении всех
Коэффициент детерминации, который получается при включении всех ![]() регрессоров;
регрессоров;
![]() Квадрат вычисленного значения
Квадрат вычисленного значения ![]() Статистики для
Статистики для ![]() Го регрессионного коэффициента;
Го регрессионного коэффициента;
![]() Длина ряда наблюдений;
Длина ряда наблюдений;
![]() Количество регрессоров;
Количество регрессоров;
![]() Число степеней свободы.
Число степеней свободы.
Расчетное значение ![]() Статистики для
Статистики для ![]() Го регрессионного коэффициента при
Го регрессионного коэффициента при ![]() может быть определено по формуле:
может быть определено по формуле:
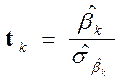 .
.
В нашем примере регрессии: ![]() исходными данными являются[5]:
исходными данными являются[5]:
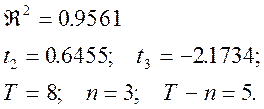
На основе этих данных, осуществим расчет частных коэффициентов детерминации для каждого из регрессоров.
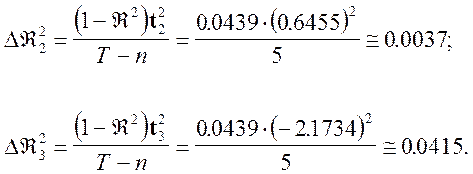
Таким образом, если из данной регрессии, при прочих равных условиях, будет исключен регрессор ![]() , то
, то ![]() уменьшится на величину
уменьшится на величину ![]() и станет равным
и станет равным ![]() . При этом в уравнении регрессии останутся только первый и третий регрессоры.
. При этом в уравнении регрессии останутся только первый и третий регрессоры.
С другой стороны, если из уравнения регрессии исключить третий регрессор, а при этом второй регрессор сохранить, то будет наблюдаться следующая картина. ![]() уменьшится на величину
уменьшится на величину ![]() и станет равным
и станет равным ![]() .
.
В случае простой регрессии ![]() величинами, необходимыми для расчета
величинами, необходимыми для расчета ![]() , являются:
, являются:
![]()
Найдите самостоятельно величину ![]() и убедитесь в том, что в простой регрессии
и убедитесь в том, что в простой регрессии ![]() (вычисления провести с учетом погрешности округления).
(вычисления провести с учетом погрешности округления).
Осуществите аналогичные расчеты на случай простой регрессии ![]() . Здесь
. Здесь ![]()
I. 8. Скорректированные коэффициенты детерминации
Одним существенным недостатком коэффициента детерминации ![]() Является то, что при включении в модель дополнительного регрессора он никогда не уменьшается, а во многих случаях — увеличивается, а это, в свою очередь, приводит к тому, что будет отдано предпочтение варианту уравнения с очень многими регрессорами. С каждым дополнительным регрессором теряется одна степень свободы и этот недостаток не учитывается с помощью
Является то, что при включении в модель дополнительного регрессора он никогда не уменьшается, а во многих случаях — увеличивается, а это, в свою очередь, приводит к тому, что будет отдано предпочтение варианту уравнения с очень многими регрессорами. С каждым дополнительным регрессором теряется одна степень свободы и этот недостаток не учитывается с помощью![]() , когда он выступает в качестве критерия выбора. С корректированные коэффициенты детерминации призваны учитывать этот факт.
, когда он выступает в качестве критерия выбора. С корректированные коэффициенты детерминации призваны учитывать этот факт.
|
Из двух вариантов уравнений, которые отличаются величиной скорректированного коэффициента детерминации, но имеют одинаково хорошие другие критерии качества, предпочитают вариант с большим значением скорректированного коэффициента детерминации. |
Скорректированный коэффициент детерминации по Тейлу: ![]() :
:
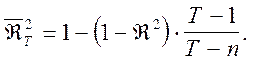
II. Скорректированный коэффициент детерминации по Амемии: ![]() .
.
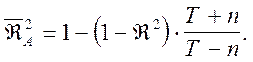
К основным свойствам скорректированных коэффициентов детерминации относятся следующие:
Оба скорректированных коэффициента легко вычисляются по приведенным выше формулам при заданном значении ![]() ;
;
Изменение обоих скорректированных коэффициентов детерминации![]() и
и ![]() , вызванное дополнительным регрессором, Может быть как положительным, так и отрицательным;
, вызванное дополнительным регрессором, Может быть как положительным, так и отрицательным;
![]() отражает потерю степеней свободы при включении дополнительного регрессора более четко, чем
отражает потерю степеней свободы при включении дополнительного регрессора более четко, чем ![]() . Это значит, что
. Это значит, что ![]() изменяется на большую величину, чем
изменяется на большую величину, чем ![]() , при включении дополнительного регрессора. Поэтому тот, кто применяет
, при включении дополнительного регрессора. Поэтому тот, кто применяет ![]() вместо
вместо ![]() в качестве критерия выбора, будет (при прочих равных условиях) отдавать предпочтение уравнению, содержащему меньшее количество регрессоров.
в качестве критерия выбора, будет (при прочих равных условиях) отдавать предпочтение уравнению, содержащему меньшее количество регрессоров.
[1] При имеем случай простой регрессии, а при регрессия множественная.
[2] Непременное условие: длина рядов должна быть больше количества регрессоров
[3] Одна из предпосылок адекватности математической модели данного типа:
[4] Одношаговый метод наименьших квадратов.
[5] Рекомендуем самостоятельно осуществить вычисление статистики для 2-го и 3-го регрессоров.