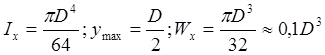Механика материалов и конструкций(ММК)

Общие положения ММК.

Все твердые тела обладают свойствами прочности и жесткости. Их изучением занимается наука, называемая механикой твердого тела, а учебная дисциплина носит название сопротивления материалов или ММК.

Прочность— это свойство оказывать сопротивление внешнему воздействию, не разрушаясь.

При расчетах на прочность определяют минимально необходимые размеры тела при которых оно не разрушается под действием внешних нагрузок.

Жесткость— это свойство материала или конструкции получать значительные деформации при действии внешних сил. При расчетах на жесткость разрабатываются такие методы, которые позволяют устанавливать зависимость между действующими нагрузками и возникающими деформациями.

Упругость— это свойство материала или конструкции возвращаться к своим первоначальным размерам и форме, после снятия внешней нагрузки.

Пластичный материал— материал, который получает значительные остаточные деформации после снятия нагрузки.

В дальнейшем все материалы условимся рассматривать, как абсолютно упругие и как однородные.

Однородность— это независимость свойств от величины выделенного объема.

Все материалы считаются изотропными.

Изотропия— независимость свойств ориентации выделенного элемента. Противоположные свойства — Анизотропия.

С геометрической точки зрения все тела мы будем разделять на 3 разновидности:

1. Брус (стержень, балка)

2. Оболочка (пластина)

3. Массив.

Брус— это тело, одно из измерений которого (длина) значительно превышает два других измерения (размеры сечения).

Брус, работающий на растяжение или сжатие, называется Стержнем.

Прямолинейный брус, работающий на изгиб, называется Балкой.

Оболочка— это тело, одно из измерений которого (толщина стенки) значительно меньше двух других.

Массив— это тело, у которого все три размера равноценны (куб).

Помимо расчетов на прочность и жесткость сжатые элементы конструкции рассчитывают на устойчивость.

Устойчивость— это свойство тела сохранять первоначальную прямолинейную форму равновесия при действии сжимающей нагрузки.

Триада расчетов, включающая в себя расчеты на прочность, жесткость и устойчивость, называется Прочным расчетом конструкции.

I.  Классификация внешних сил.

Все внешние нагрузки делят на:

Поверхностные и объемные.

Объемными называются силы, приложенные к каждой единичке объема тела: гравитационные, силы инерции, силы магнитного притяжения.

Поверхностные силы делятся на 4 вида:

1.  Силы давления— сила, приходящаяся на единицу площади. 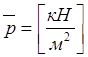(давление пара).

2.  Погонные силы— приходящиеся на единицу длины.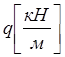

3.  Сосредоточенные силы

4.  Сосредоточенный момент

Во многих случаях P и M являются результатом приведения распределенных на небольшом участке сил к одной точке.

Правило приведения погонных сил к одной точке:

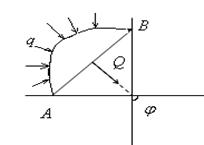
1). Требуется провести Q к точке А.

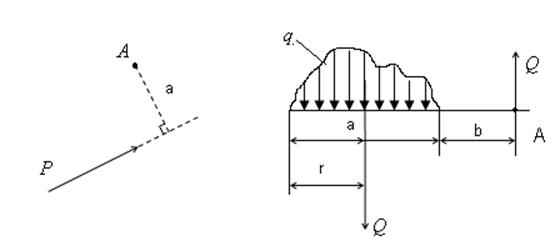
Задача решается в два этапа:

Погонная нагрузка заменяется её равнодействующей. Равнодействующая сил приложена в центре тяжести эпюры нагрузки и равна площади этой эпюры.

Результаты приведения — это моменты М и сила .

2). Требуется определить проекцию равнодействующей сил давления на ось T.

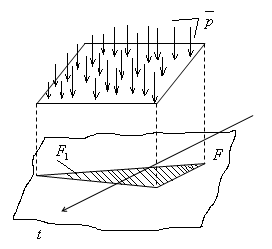
1.  Проводим плоскость перпендикулярно оси t.

2.  Проецируем поверхность на плоскость .

3. 

3). Для оболочек:

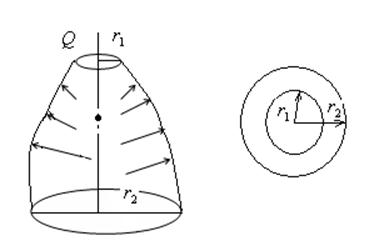
4). Требуется найти равнодействующую погонных сил:

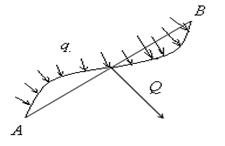
5).

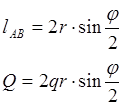
Все внешние силы делят на активные и пассивные.

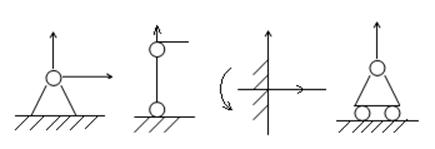— реакции опор.

После того как реакции определены, они включаются в число внешних сил. Постановка дополнительных опор в конструкции как правило делает систему более жесткой и более прочной.

Все конструкции делят на статические определимые и статически неопределимые.

Статически определимая — это система, в которой все реакции опор могут быть определены только из уравнений равновесия.

Виды деформаций под действием внешних сил:

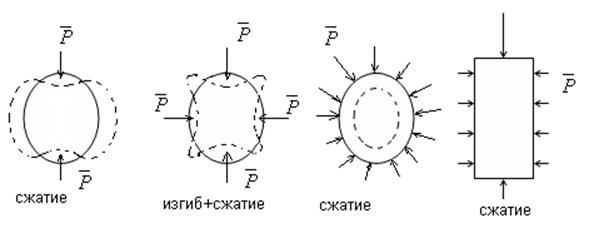
С точки зрения прочности наилучшим видом деформации является сжатие или растяжение, но не изгиб. При изгибе резко изменяется форма и кольцо потеряет устойчивость.

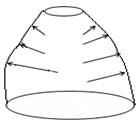Оболочка является идеальной с точки зрения прочности и устойчивости конструкции. Она способна работать только на сжатие или растяжение, в ней не возникает изгибающих моментов.

III. Внутренние силы в сечении. Метод сечения.

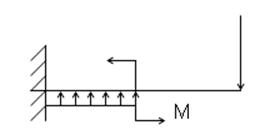— по внешним нагрузкам нельзя сказать где произойдет разрушение конструкции. Критерием разрушения являются внутренние силы.

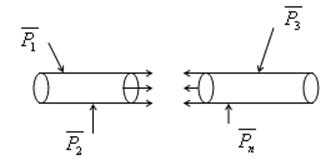
Пусть брус находится в равновесии. Разрежем его в интересующем нас месте (мысленно).

Если спроектировать И на оси координат, то получим три проекции силы и три момента — ВСФ (внутренние силовые факторы).

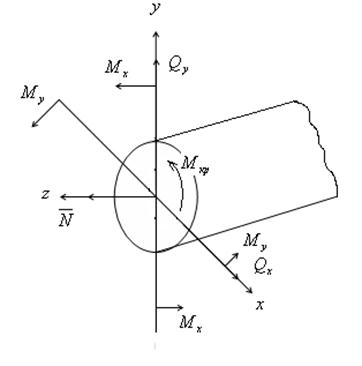В произвольном сечении бруса в общем случае возникает 6 ВСФ. Где:

N — осевое, нормальное усилие, вызывает деформацию растяжения, сжатия.

— поперечные или перерезающие, они вызывают деформацию сдвига или среза.

— вызывают изгибающий момент (вертикальный или горизонтальный).

— крутящий момент.

Правило ВСФ:

Любой из 6 ВСФ численно равен алгебраической сумме соответствующих внешних сил, приложенных к отброшенной части системы.

Для определения усилия N нужно все внешние силы, отброшенной части системы, спроецировать на ось z и взять их алгебраическую сумму.

Для определения нужно вычислить моменты всех сил отброшенной части системы относительно оси x и взять их алгебраическую сумму.

При переходе от одного сечения бруса к другому, в общем случае все 6 ВСФ изменяют свои значения.

График, показывающий законы изменения любого из 6 ВСФ по длине бруса, называют Эпюрой этого ВСФ.

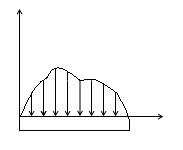
Правило построения эпюр ВСФ.

1.  Определяют опорные реакции.

2.  Конструкцию разбивают на участки: границами участков служат точки приложения сосредоточенных сил и моментов, границы распределенной нагрузки, точки резкого изменения геометрии системы.

3.  В произвольном сечении z каждого участка записывают уравнения равновесия соответствующих ВСФ в виде x(z), где .

4.  по уравнению вычисляют ряд значений ВСФ в пределах данного участка и по результатам строят эпюру на данном участке.

Правило знаков для ВСФ.

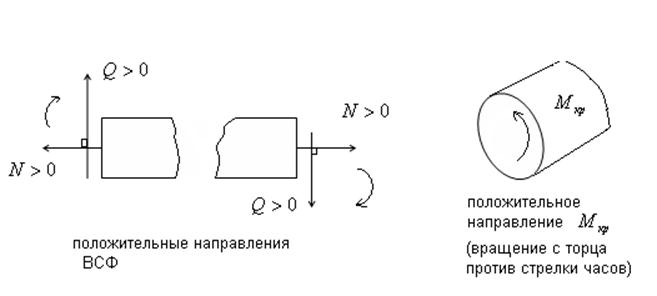
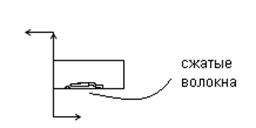
При записи уравнений изгибающих моментов принимаем произвольное правило знаков, а эпюру будем откладывать со стороны сжатых волокон.

В зависимости оттого, какие ВСФ отличны от нуля, различают следующие простые деформации:

1. — растяжение, сжатие.

2. — кручение.

3. — сдвиг, срез (чистый).

4.

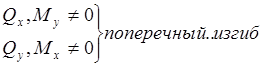
Сложные деформации.

1. — неплоский изгиб.

2. — поперечный изгиб + растяжение.

3. — неплоский изгиб с кручением.

Качественный анализ стержневой системы.

Стержневые системы делят на плоские и пространственные.

Плоская система— геометрически плоская и имеет нагрузку в этой же плоскости. Если система геометрически плоская, а нагрузка перпендикулярная этой плоскости называется Плоскостно-пространственной.

Все системы делят на статически определимые и статически неопределимые. У статически определимой системы все реакции опор определяются только из уравнений равновесия.

Связи бывают внешние и внутренние. Внешние связи накладываю ограничения на линейные или угловые перемещения отдельных точек системы. Реализуются в форме опор. Внутренние связи накладывают ограничения на взаимные смещения точек системы.

Всякий замкнутый контур плоской системы накладывает на неё три внутренние связи. Любой контур пространственной системы накладывает на неё 6 внутренних связей.

Связи, обращающие систему в статически определимую и кинематически не изменяемую, называются Необходимыми.

Степень статически определимой системы может определяться по следующей формуле:

СН = ВШ + ВН – ШР – НХ

Где ВШ — внешние связи,

ВН — внутренние связи,

ШР — шарниры,

НХ — необходимые связи.

Деформация растяжения и сжатия.

Напряжение— числовая мера распределения внутренних сил по сечению .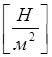

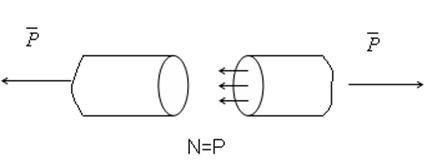
Для однородного стержня внутренние силы распределены по сечению равномерно. Тогда нормальное напряжение для всех точек сечения будет равно:

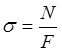— при растяжении-сжатии

Где F — площадь поперечного сечения.

Закон Гука при растяжении-сжатии.

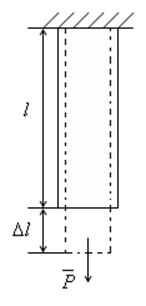
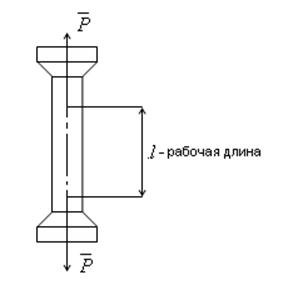
Дан стержень длиной l, к нему приложили нагрузку P.

— абсолютное удлинение стержня.

— относительное удлинение стержня.

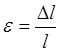
В пределах малых удлинений для большинства материалов справедлив закон Гука, который устанавливает прямую пропорциональность между напряжениями и деформациями:

Е — модуль упругости I ряда (модуль Юнга)

Е – является физической характеристикой материала и определяется экспериментально для каждого материала.

Физический смысл:

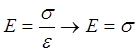при

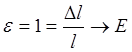является напряжением, которое возникло бы в стержне при увеличении его в два раза.

Для стали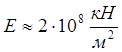

Е — берется по справочникам для различных материалов.

Потенциальная энергия деформации.

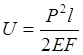
Если реакция N изменяется вдоль стержня, то

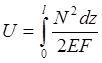; — участки стержня.

Закон Пуассона.

Наблюдения показываю, что удлинение стержня в осевом направлении сопровождается уменьшением его поперечных размеров. Таким образом, при растяжении (сжатии) возникает не только продольная, но и поперечная деформация стержня:

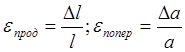
Экспериментально установлено, что в пределах применимости закона Гука, поперечная деформация пропорциональна продольной.

— безразмерный коэффициент (коэффициент Пуассона)

— определяется по таблицам

— для пробкового дерева.

— для мягкой резины.

Определение упругих удлинений.

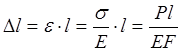
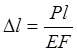— при однородном напряженном состоянии.

В случае термоупругого напряженного состояния (наличие температуры):

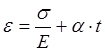
Где — коэффициент температурного расширения материала.

Тогда:

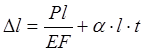
Диаграмма растяжения мягкой стали и основные характеристики материала.

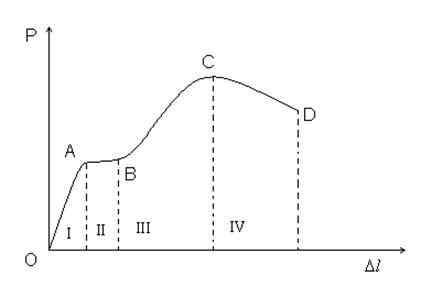
I – зона упругости (справедлив закон Гука и 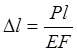) удлинение очень малы

II -зона общей текучести материала. Сила постоянна при росте деформации на всей рабочей длине. АВ — площадь текучести.

III— зона упрочнения. Здесь удлинение образца сопровождается возрастанием нагрузки, но неизмеримо более медленным (в сотни раз), чем на упругом участке. В стадии упрочнения на образце образовывается местное сужение — место будущего разрыва.

IV – зона местной текучести. Удлинение образца происходит с уменьшением силы. Точка D соответствует разрушению образца.

Перестроим диаграмму в координатах и .

1.  Наибольшеё напряжение, до которого материал следует закону Гука, называется пределом пропорциональности ().

2.  упругие свойства материала сохраняются до напряжения, называемого пределом упругости. Под пределом упругости () понимается такое наибольшеё напряжение, до которого материал не получает остаточных деформаций.

3.  Предел текучести – () напряжение, при котором происходит рост деформации без заметного увеличения нагрузки. ( — при растяжении и сжатии соответственно).

4.  Отношение максимальной силы, которую способен выдержать образец, к его начальной площади поперечного сечения, носит название предела прочности — (растяжение) и (сжатие).

Для всех материалов эти пределы приводятся в справочных таблицах.

Эти данные используются для расчетов на прочность.

Основным и более распространенным является метод расчета по напряжениям.

Расчет ведется по наибольшему напряжению , возникающему в некоторой точке напряженной конструкции. Напряжение называется максимальным рабочим напряжением. Оно не должно превышать определенной величины, свойственной данному материалу и условием работы конструкции.

— допускаемое напряжение (таблицы).

Кручение.

При кручении имеют место касательные напряжения — .

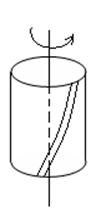
Под кручением понимается такой вид напряжения, при котором в поперечных сечениях стержня возникает только крутящий момент.

Для кручения:

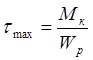
Где — крутящий момент

— полярный момент сопротивления

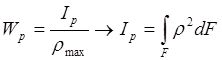— полярный момент инерции сечения. Геометрическая характеристика.

Для валов (сплошного сечения):

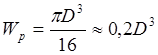
Для полых валов:

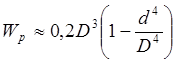
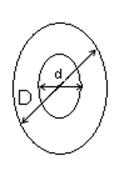
— допускаемое напряжение (по таблицам).

Изгиб.

Под изгибом понимается такой вид напряжения, при котором в поперечных сечениях стержня возникают изгибающие моменты.

Сопротивление при изгибе:

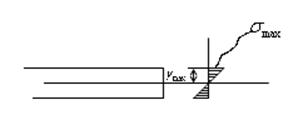
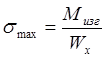
Где 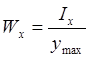— момент сопротивления при изгибе.

— момент инерции сечения.

Для стержня прямоугольного сечения со сторонами b и h:

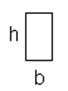
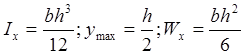
Для стержня круглого сечения: