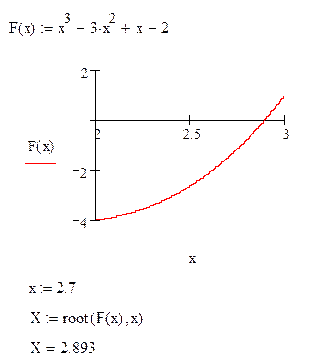Задание: Методами: деления пополам, касательных, методом хорд на интервале изменения независимой переменной от 2-х до 3-х с точностью до 10-5 уточнить корень уравнения x3 – 3×2 + x – 2 = 0.
Метод деления пополам
Метод решения: Метод заключается в постоянном делении отрезка интервала функции на 2. Деление продолжается до тех пор пока функция не будет стремиться к 0. Данный метод позволяет найти корень уравнения с заранее заданной точностью.
Алгоритм:
Sub dtomial()
A = Range("B1")
B = Range("B2")
Eps = ("B3")
If f(a) * f(b) < 0 Then
i = 1
Do
x = (a + b) / 2
If f(x) * f(a) < 0 Then
b = x
ElseIf f(x) * f(a) > 0 Then
a = x
Else
Cells(i, 4) = x
Exit Do
End If
Cells(i, 4) = x
i = i + 1
Loop While Abs(a — b) > eps
Else: Range("D1") = "Корней нет"
End If
End Sub
Function f(x)
f = x ^ 3 — 3 * x ^ 2 + x — 2
End Function
Метод касательных.
Метод решения Заключается в построении касательной в точке А. Далее откладывается перпендикуляр от касательной на функцию. Из точки, полученной после проведения перпендикуляра проводим еще одну касательную.. Метод повторяется до тех пор пока будет справедливо неравенство:![]() .
.
Алгоритм:
Sub Newton()
A = Range("B1")
B = Range("B2")
Eps = ("B3")
Delta = Range("b4")
I = 1
Do
If f(a) * f1(a, delta) > 0 Then
DX = f(a) / f1(a, delta)
x = a — DX
a = x
Else
DX = f(b) / f1(b, delta)
x = b — DX
b = x
End If
Cells(i, 5) = x
i = i + 1
Loop While Abs(DX) >= eps
End Sub
___________________________
Function f(x)
f = x ^ 3 — 3 * x ^ 2 + x — 2
End Function
___________________________
Function f1(x, delta)
F1 = (f(x + delta) — f(x)) / delta
End Function
___________________________
Function f2(x, delta)
F2 = (f1(x + delta) — f1(x)) / delta
End Function
Проверка решения в MathCAD.