Логарифмические частотные характеристики
Чаще всего амплитудную и фазовую частотные характеристики изображают в логарифмическом масштабе. Такие логарифмические частотные характеристики очень удобны для инженерных расчетов.
При построении логарифмической амплитудной частотной характеристики (ЛАЧХ) по оси ординат откладывают величину
L(W)=20lgA(W)=20lgïW(jW)ï,
Единицей измерения для которой является децибел (дБ). По оси абсцисс откладывается частота W ![]() в логарифмическом масштабе (рис.8).
в логарифмическом масштабе (рис.8).
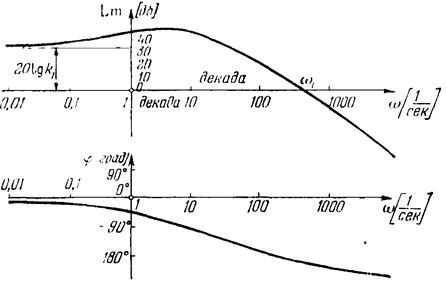
Рис.8. Логарифмические частотные характеристики.
Равномерной единицей на оси абсцисс является декада — любой отрезок, на котором значение частоты увеличивается в десять раз. Точка пересечения ЛАЧХ с осью абсцисс называется частотой среза WСр.
Начало координат обычно помещают в точке W=1, так как Lg1=0. Точка же W=0 лежит в —¥. Однако, в зависимости от интересующего нас диапазона частот можно начало координат брать и в другой точке (W=0,1; W=10 или др.)
При построении логарифмической фазовой частотной характеристики (ЛФХ) отсчет углов Y идет по оси ординат в обычном масштабе в угловых градусах. По оси абсцисс частота W откладывается по-прежнему в логарифмическом масштабе.
Важно иметь в виду, что ось абсцисс (L=0) соответствует значению А=1, т. е. прохождению амплитуды сигнала через звено без изменения амплитуды. Верхняя полуплоскость ЛАЧХ соответствует значениям А>1 (усиление амплитуды), а нижняя полуплоскость — значениям А<1 (ослабление амплитуды).
2. Основные типы звеньев.
Типы звеньев систем автоматического управления и регулирования различаются в зависимости от вида их передаточных функций (или дифференциальных уравнений), определяющих их динамические свойства и характеристики.
Типовые динамические звенья характеризуются дифференциальными уравнениями, порядок которых не выше второго.
В зависимости от вида дифференциальных уравнений в теории автоматического управления различают следующие основные типовые звенья:
-безынерционное (пропорциональное или усилительное);
-инерционное первого порядка (или апериодическое);
-инерционное второго порядка;
-интегрирующее;
-дифференцирующее;
-реальное дифференцирующее;
-колебательное;
-звено запаздывания.
Основные типы звеньев делятся на три группы:
-позиционные;
-дифференцирующие;
-и интегрирующие.
Позиционными звеньями называются такие, в передаточной функции которых
W(Р)=k×=×
Многочлены Bm(p) и An(p) имеют свободные члены равные 1, т. е. эти звенья обладают статической характеристикой Yуст=k×Xуст (при Р=0 W(р)=k=), определяющей их состояние равновесия — свойство позиционности.
У Дифференцирующих звеньев в выражении передаточной функции отсутствует свободный член числителя, т. е. для однократно дифференцирующего звена будет B0=0:
W(р)= = ×=k×Р,
Где Bm-1(p) имеет свободный член, равный 1, а K= – коэффициент усиления.
Передаточные функции Интегрирующих звеньев имеют соответственно вид:
W(р)= = ×=×,
Где An-1(p) имеет свободный член, равный 1.
Для двукратно интегрирующего звена A0=A1=0
W(р)= = ×=×,
Знание характеристик типовых звеньев необходимо для расчетов систем управления.
2.1. Идеальное усилительное (безынерционное) звено.
Уравнение и передаточная функция звена:
Y(T)=K×X(T), W(P)=K.
Примерами безынерционного звена являются редуктор, делитель напряжения, датчики угла, безынерционный усилитель и др. (рис.9).
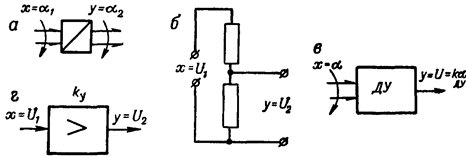
Рис. 9. Примеры безынерционных звеньев.
В действительности безынерционных звеньев нет. Обычно в САР идеальными считают звенья, инерционность которых значительно меньше инерционности других звеньев. Чаще всего это различные датчики и предварительные усилители. Инерционное запаздывание многих измерительных элементов автоматических систем (датчиков угла рассогласования, фотоэлектрических датчиков, магнитоэлектрических датчиков) мало, поэтому их считают безынерционными звеньями.
Амплитудная и фазовая частотные характеристики (рис.10): A(W)=K; Y(W)=0.
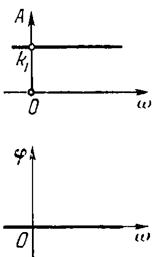
Рис.10. Частотные характеристики безынерционного звена
Переходная функция звена: H(T)=K, T>0.
2.2. Инерционное (апериодическое) звено.
Уравнение и передаточная функция звена:
(Тр+1)Y(P)=KX(P); W(P)=,
Где Т – постоянная времени; K – коэффициент передачи звена.
Примерами инерционных (апериодических) звеньев являются двигатели постоянного тока, если Х(t) — напряжение питания, а Y(t) — угловая скорость вала W(t); двухфазные асинхронные двигатели; усилители при учете инерционного запаздывания; массивное тело, если входной величиной считать количество поступающего в единицу времени тепла Q, а выходной — температуру в какой-либо точке внутри тела и др.); L-R цепочка (рис.11).
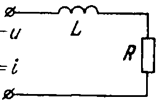
Рис.11. Пример инерционного звена.
Амплитудно-фазовая частотная характеристика: W(JW)= (рис.12).
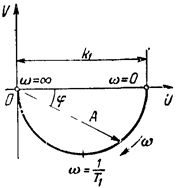
Рис.12. АФЧХ инерционного звена.
Из W(JW) находим: A(W)=, Y(W)=-ArctgWT.
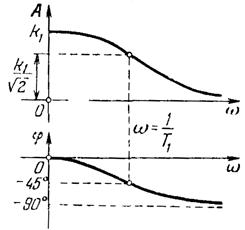
Рис.13. Амплитудно-частотная и фазо-частотная характеристики инерционного звена
Логарифмическая амплитудно-частотная характеристика имеет вид:
L(W)=20lg=20lgk-20lg.
Эта характеристика имеет асимптоты:
А)при W®0 L(W)®20lgk;
Б)при W®¥ L(W)®20lgk-20lgTW.
Последняя асимптота будет наклонной прямой с наклоном -20 дБ/дек, а первая – горизонтальная прямая. Пересекаются асимптоты в точке Wс=. Сама ЛАЧХ близка к этим асимптотам.
На логарифмической сетке по оси частот откладывается сопрягающая частоте Wс= (рис.14). Для частот меньших, чем сопрягающая, т. е. при W<, можно пренебречь вторым слагаемым под корнем, тогда левее сопрягающей частоты можно заменить L(W) приближенным выражением
L(W)»20lgk.
Этому выражению соответствует горизонтальная прямая. Для частот больших сопрягающей W> в выражении для L(W) можно пренебречь 1 под корнем. Тогда L(W)=20lgk-20lg(WT). Второе слагаемое представляет собой прямую линию, идущую под наклоном -20 дБ/дек. Ломаная линия и называется асимптотической ЛАЧХ. Наибольшее отклонение точной ЛАЧХ от асимптотической приблизительно равно 3 дБ на частоте сопряжения, т. к.:
DL()=20lgk-20lg=20lgk-3,03 (дБ).
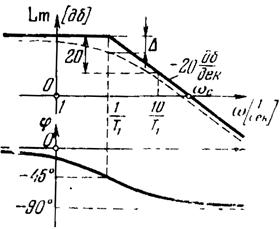
Рис.14. ЛАЧХ инерционного звена.
Переходная функция, согласно решению уравнения звена, при Х(t)=1(t) и нулевых начальных условиях имеет вид (рис.15):
H(T)=K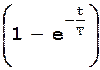 .
.
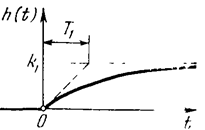
Рис.15. Переходная функция инерционного звена.
Постоянная времени Т определяет наклон касательной в начале кривой (рис.15). Следовательно, величина Т характеризует степень инерционности звена, т. е. длительности переходного процесса. Теоретически такой переходный процесс длится бесконечно долго. Практически для этого звена под временем переходного процесса понимают промежуток времени Tп по истечении которого выполняется неравенство:
1-h(tп)£D,
Где D — наперед заданное положительное число (обычно D=0,01¸0,05).
При подаче на вход звена постоянного сигнала X0 По окончании переходного процесса координата Y(t) Жестко связана с входной:
YУст=Y(¥)=Kx0.
2.3. Колебательное звено.
Уравнение и передаточная функция звена:
(T22p2+T1p+1)Y(p)=kX(p), W(p)=,
Причем предполагается T1<2Т2, так что корни характеристического уравнения T22P2+T1P+1=0 — комплексные.
Общепринята запись передаточной функции колебательного звена в виде:
W(P)=,
Где Т=T2, X= причем 0<X<1, так как T1<2Т2. При X³1 звено становится инерционным звеном второго порядка.
Амплитудно-фазовая частотная характеристика (рис.16) звена:
W(JW)=, A(W)=, Y(W)=-Arctg.
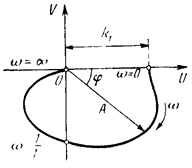
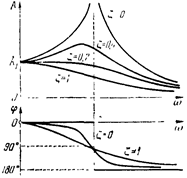
Рис.16. Частотные характеристики колебательного звена.
Амплитудная характеристика уменьшается с увеличением W, т. е. А(W)£K, если 1>X>0,707. При X<0,707 появляется максимум на характеристике А(W), который уходит в бесконечность при X®0. Поэтому величина X= называется параметром затухания. Отсюда видна роль постоянных времени Т1 и Т2 в уравнении звена: постоянная Т2 увеличивает колебания, а T1 — демпфирует их.
Логарифмическая амплитудная частотная характеристика звена
L(W)=20Lgk-20Lg.
При значениях 0,5<X<1 характеристика близка к ломаной (рис.17).
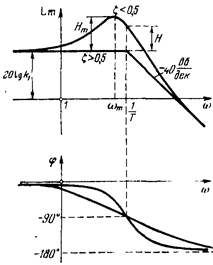
Рис.17. Логарифмические частотные характеристики колебательного звена.
Если же X<0,5, то получается заметный максимум (рис.17). Максимум характеризуется превышением Hm
Hm=20Lg
На частоте
WM=.
В упрощенных расчетах достаточно находить Hm приближенно (см. рис.17):
Hm»20Lg при W=.
Переходная функция колебательного звена изображена на рис.18.
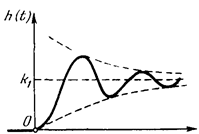
Рис.18. Переходная функция колебательного звена.
Она имеет вид:
H(T)= .
.
При X=1 колебания вырождаются в апериодический процесс.
При X=0 колебания становятся незатухающими (периодическими), и в этом случае колебательное звено носит название консервативного звена.
Примеры колебательных звеньев изображены на рис.19.
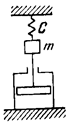
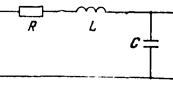
Рис.19. Примеры колебательных звеньев