Почвенная влага
1. Состав и свойства воды
Давно заметили, что вода – соединение, отличающееся необыкновенными свойствами (А. Крафтс, Х. Карриер, К. Стопинг, 1951). Она занимает исключительное положение по величине теплоты парообразования, имеет достаточно высокую теплоту плавления, большие показатели поверхностного натяжения, большие показатели поверхностного натяжения, внутреннего давления.
Молекула воды состоит из водорода, который при температуре минус 253˚С и давлении в 1 атм, и кислорода, который кипит при минус 180˚С; вода при таком давлении кипит при 100˚С. Если бы вода не была аномальной жидкостью, то она не должна была бы иметь низкую температуру кипения, равную по расчётам от минус 65 до минус 100˚С. Температура замерзания воды должна бы находится примерно в пределах от минус 100 до минус 150˚С. Аномальные свойства воды проявляются также в том, что её теплоёмкость имеет минимальное значение при 37,5˚С, плотность наибольшая при 4˚С, а коэффициент расширения наивысший в твёрдом состоянии.
Соответственно современным представлениям, вода (окись водорода) Н2О – наиболее простое химическое соединение водорода с кислородом — состоит из молекул – диполей с положительным и отрицательным зарядами. При соприкосновении с телами (поверхностями), например, с почвенными частичками, которые имеют электрическое поле, диполи воды поляризуются (ориентируются), поворачиваясь до поверхности заряженного тела, зависимо от знака его заряда, положительным или отрицательным полюсом. При этом, поляризуючись внутри себя, диполи воды могут образовывать цепочки. Поэтому наряду с простыми молекулами, она может содержать и более сложные молекулярные агрегаты с двух-трёх и больше молекул. Такие агрегаты постоянно возникают и опять распадаются.
Причиной возникновения молекулярных агрегатов есть водородные связи Томпсон Л. И. и Троу Ф. Р., 1982). Поэтому изучение структуры воды и особенно возникновение и разрушение водородных связей позволит понять свойства этой удивительной жидкости. Причиной возникновения водородных связей объясняются особенностью строения молекулы воды. Дело в том, что атомы водорода в молекуле воды не расположены ни вместе, как это представляется из формулы Н2О, на противоположных сторонах атома кислорода, о чём можно припустить исходя из формулы НОН.
Молекула воды представляет собой тетраэдр с четырьмя полюсами на его вершинах: два с них несут положительные заряды, и два – отрицательные. Центр тетраэда соответствует центру молекулы воды
Атом кислорода имеет сильную электропроницаемость и стремится оттянуть электроны от атомов водорода. Благодаря этому на атоме кислорода возникает частично отрицательный заряд, в тоже время два атома водорода приобретают частично положительного заряда. Атомы водорода воды, которые несут положительный заряд, зазнают электрического притяжения со стороны отрицательно заряженных атамов кислорода соседних молекул воды. Это и приводит к возникновению водородных связей между молекулами. В следствии такого связывания молекул воды одна с одной имеет место большая их упорядоченность в водных растворах. На отдельных участках воды приобретает почти кристаллическую структуру, что очень важно, поскольку может играть решающую роль во взаимодействии и ориентации молекул в водных растворах.
Результаты определения молекулярной массы водяной пары показывают, что она практически состоит из свободных молекул воды (Н2О) или гидрола. Лёд состоит из молекул тригидрола (Н2О)3, а жидкая вода представляет собой смесь дигидроля (Н2О)2 и тригидроля (Н2О)3. Соотношение количества этих двух видов молекул в жидкой воде изменяется в зависимости от температуры. По расчётам Сатерленда (А. Крафтс, Х. Карриер, К. Стонинг, 1951), при 0˚С доля молекул воды (Н2О)3 в воде составляет 0,375 от всего количества молекул; при 20˚С эта величина равна 0,321; при 40˚С – 0,284; при 60˚С – 0,255; при 80˚С – 0,234; при 100˚С – 0,203. При 4˚С частички (Н2О)3 составляют примерно 1/3, а частички (Н2О)2 – 2/3 всего количества молекул.
В водяной паре водородных связей практически нет. При таянии льда разрывается около 15%, а при нагревании воды до 40˚С – около половины всех водородных связей.
Таким образом, вода, невзирая на просту её химическую формулу, довольно сложное вещество и по своим свойствам значительно отличается от других жикостей.
Энергетика почвенной влаги
2.1. Взаимодействие воды с почвой
Почва представляет собой представляет собой трёхфазную систему и состоит из твёрдой, жидкой и газообразной систем. Твёрдая фаза есть дисперсным телом и состоит из мелких и мельчайших частиц минералов и органических веществ. С дисперсностью почвы связаны две важнейшие её свойства: удельная поверхность и пористость, а отсюда и поверхностная энергия почвенных частичек.
Молекулы воды представляют собой диполи с положительным зарядом (ион Н+) на одном конце и отрицательным (0-) на противоположном. Наличие неодинаковых зарядов на диполях есть причичиной того, что молекулы воды вступают в определённые связи между собой, а также с ионами диссоциированных в воде веществ и частичками почвы. Вследствие этого, как в самой воде, так и на разделе вода – твёрдая фаза и вода – воздух возникают сложные явления, которые в значительной мере определяют поведение почвенной влаги. Причиной этих явлений, которые на поверхности раздела фаз называются Поверхностными явлениями, есть то, что состояние веществ поверхности раздела соприкосновения фаз отличается от их состояния внутри этих фаз вследствие разных молекулярных полей в разных фазах.
В поверхностных явлениях берут участие только те молекулы, которые находятся на поверхности тел. Если размеры тел достаточно больше, то число таких молекул совсем небольшое по сравнению с числом молекул в основном объёме. Поэтому поверхностные явления в больших объёмных тел не играют заметной роли. Но в дисперсных телах, к которым принадлежит и почва, при наличии частичек малых размеров они стают решающими. Все свойства почв и процессов, которые в них протекают, прямо или посредственно в той или иной мере связаны с поверхностными явлениями. Остановимся на основных из них и рассмотрим их физическую природу.
2.2. Поверхностное натяжение
Поверхностное натяжение обуславливается силами притяжения между молекулами. На каждую молекулу жидкости действуют силы притяжения со стороны окружающих молекул, отдалённых от неё на расстояние, не превышающее 1,5 · 10-7 см, т. е. которые находятся (центрами) в средине сферы радиусом R = 1,5 · 10-7 см. Эта сфера называется сферой молекулярного действия. Так как радиус R самых молекул составляет примерно 1,5 · 10-8 см, то R = 32, т. е. радиус сферы молекулярного действия примерно равен полтора диаметрам молекулы. Таким образом, каждая молекула жидкости взаимодействует только с соседними молекулами, которые непосредственно к ней прилегают (Р. И. Грабовский, 1974).
Рассмотрим молекулу, расположенную в середине жидкости (а и б), налитой в сосуд (рис. 1). Со всех сторон её окружает в среднем одинаковое число молекул, поэтому результирующая сил притяжения, которые действуют на молекулу, в среднем равна нулю. Тоесть, в средине жидкости силы притяжения между молекулами взаимно компенсируются.
Другие условия складываются для моекул, которые лежат на поверхности жидкости (в и г). Так как концентрация молекул в расположенном над жидкостью воздуха небольшая по сравнению с концентрацией в жидкости, то результирующая сил, которые действуют на молекулу, не равна нулю и направлена в средину жидкости перпендикулярна её поверхности. В таком же положении находятся все молекулы, которые лежат в поверхностном слое жидкости толщиной, примерно равной радиусу сферы молекулярного действия.
Таким образом, поверхностный Мономолекулярный слой жидкости толщиной 1,5 · 10-7 см совершает на всю жидкость давление, равное сумме результирующих сил. Это давление называется Внутренним Или Молекулярным. Поэтому, чтобы переместить молекулу с глубины на поверхность жидкости, необходимо свершить работу против результующей силы. В результате молекулы на поверхности жидкости имею определённую потенциальную энергию, которую называют Поверхностной энергией.
Благодаря тому, что молекулы жидкости находятся близко одна от другой, жидкость мало сжимается: силы отталкивания между молекулами, которые вступают в действие на очень малых расстояниях, препятствуют сжатию жидкости.
Напряжённое состояние поверхностного слоя жидкости Называется поверхностным натяжением. Оно вызывается силами сцепления между молекулами этого слоя, численно равное работе, которое необходимо совершить для того, чтобы при постоянной температуре увеличить на единицу площади поверхность раздела воды и её насыщенного пара, поднять молекулу воды из середины в поверхностный слой. Выделим мысленно в поверхностном слое воды круговой контур длиной L
Молекулы воды, которые составляют контур, притягиваются молекулами, расположенными в средине контура; Силы притягивания касательным до поверхности воды и перпендикулярные контуру. Сумма сил притяжения, которые действуют на контур, который ограничивает поверхность воды, называется Силой поверхностного натяжения F. Эта сила пропорциональна числу молекул, которые притягиваются к контуру, которые в свою очередь очень пропорциональны длине контура; таким образом,
![]() (1)
(1)
где ![]() — коэффициент пропорцийности, который называется коэффициентом поверхностного натяжения.
— коэффициент пропорцийности, который называется коэффициентом поверхностного натяжения.
Коэффициентом поверхностного натяжения (![]() ) воды равный силе поверхностного натяжения, которая действует на единицу длины контура, ограничивающего поверхность воды. Измеряется в джоулях на квадратный метр (Дж/м2) или ньютонах на метр (Н/м).
) воды равный силе поверхностного натяжения, которая действует на единицу длины контура, ограничивающего поверхность воды. Измеряется в джоулях на квадратный метр (Дж/м2) или ньютонах на метр (Н/м).
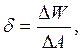 (2)
(2)
Где ![]() W – работа,
W – работа, ![]() А – изменение площади поверхности.
А – изменение площади поверхности.
Поверхностное натяжение воды при 20˚С равно 0,0727 Н/м, или 72,7 дин/см. Это наивысший показатель среди распространённых жидкостей. Для сравнения: бензол – 28,9, толуол — 28,5, этиловый спирт – 22,3 дин/см.
2.3. Силы межмолекулярного воздействия
Между молекулами действуют силы, величина которых зависит от агрегатного состояния вещества. В случае твёрдых тел и жидкости эти силы определяют объём тела. Объём тела может изменяться (уменьшатся или увеличиваться) только под влиянием внешних сил. Это значит, что молекулы расположены на некотором равновесном расстоянии одна от другой. Если расстояние между молекулами становится меньше равновесного значения, между молекулами возникают силы отталкивания, при большем расстоянии — силы притяжения. Силы межмолекулярного взаимодействия представляют собой равнодействующую сил отталкивания и притяжения, которые компенсируют одна одну при нормальном равновесном расстоянии между молекулами. Межмолекулярные силы действуют на очень малых расстояниях между молекулами, причём силы отталкивания уменьшаются при увеличении расстояния быстрее сил притягивания. Радиус действия межмолекулярных сил не превышает 10 Нм.
Межмолекулярные взаимодействия может проявляться в виде таких явлений, как сорбция и десорбция, когезия и адгезия.
Сорбция – физико-химический процесс, в результате которого происходит поглощение коллоидным телом газов, паров или растворимых веществ с окружающей среды. Если поглощение происходит поверхностью твёрдого или жидкого тела, то такое явление называется адсорбцией, а если всем объёмом твёрдого или жидкого тела – то абсорбцией. Вещества, которые поглощаются, называется адсорбтивом или адсорбатом, а жидкость или твёрдое тело, которые адсорбируют их, – Адсорбентом.
Взаимодействие между поверхностными слоями одинаковых тел называется когезией (сцепление); взаимодействие между поверхностными слоями разных тел – адгезией (прилипанием). Когезия – это сцепление молекул одногоо тела между собой, что обуславливается взаимным притяжением.
Адгезия – это прилипание молекул двух разных тел. Адгезия возникает между твёрдыми, твёрдыми и жидкими, а также жидкими и газоподобными телами.
Различают физическую и химическую адсорбцию. Первая оборотная, вторая – необоротная. На сорбцию воды почвой значительное влияние имеет природа составных частей почвы. По-разному адсорбируют воду органические и минеральные коллоиды, среда минеральных коллоидов есть почвы, которые адсорбируют воду по экстракристаллическому типу (только поверхностью кристаллов), по типу интракристаллическому без набухания (с вхождением воды во внутрь кристалла без раздвижения решётки) и по типу интракристаллическому при набухании кристаллов адсорбента (вхождения во внутрь кристалла с раздвижением пакетов ионов).
Вследствие теплового движения молекул наряду с адсорбцией происходит обратный процесс – Десорбция. Для каждой концентрации адсорбтива в окружающей среде существует состояние адсорбцийного равновесия, которое определяет количество адсорбированного вещества. Для конкретной температуры существует своё состояние адсорбцийного равновесия, а количество адсорбированного вещества в случае физической адсорбции уменьшается с повышением температуры. При адсорбции газов, как и при конденсации, выделяется тепло.
2.4. Явления смачивания
Если на гладкую поверхность твёрдого тела нанести каплю жидкости, то можно наблюдать такие эффекты: капля или остаётся на поверхности, или растекается по поверхности. Это зависит от характера взаимодействия между самыми молекулами капли и молекулами капли и поверхностью твёрдого тела. Если последние преобладают, капля растекается по поверхности, тоесть имеет место явление смачивания этой поверхности.
Способность к смачиванию поверхности твёрдого тела можно рассматривать как следствие действия поверхностных сил, которые обусловлены существованием поверхностного натяжения на границе раздела фаз. Чем слабее межмолекулярные взаимодействия в жидкости, тем меньшая разница во взаимодействии между молекулами в жидкости и с поверхностью и тем лучше она смачивает любую поверхность. Вода имеет наибольшее поверхностное натяжение, поэтому смачивает только некоторые поверхности, в том числе и почву.
2.5. Капиллярные явления
Между молекулами поверхности жидкости действуют силы притягивания (адгезии Fa). Вместе с межмолекулярными силами они приводят до возникновения Краевого угла Q между стенками сосуда и поверхностью жидкости. Равнодействующая сил когезии и адгезии Fk и Fа всегда перпендикулярна поверхности жидкости. Если Q < 90˚: жидкость смачивает стенку, Q > 90˚: жидкость не смачивает стенку. Так как вода смачивает почву то краевой угол меньше 90˚.
В узком сосуде краевые искривления охватывают всю поверхность жидкости, делая её полностью согнутой: вогнутой для смачивающей жидкости (рис. а), выпуклой для несмачивающей жидкости (рис. 3, б). Такая согнутая поверхность называется мениском.
Физическую сущность капиллярных явлений А. А. Роде (1965) описывает так. Если сосуд, в котором находится вода, имеет достаточно большой диаметр, то головная, центральная часть поверхности воды остаётся плоской, и искривляется только сам её край. Если же диаметр сосуда настолько небольшой, что он что он стаёт сопоставимым с радиусом кривизны пристенного искривлённого края поверхности воды, то эти искривленные края сливаются, и образуются мениски. Так как радиус кривизны очень небольшой, образование менисков может происходить в трубках или щелях только с малым диаметром. Такие узкие сосуды – трубки или щели называются капиллярами. Чем меньше диаметр трубок, тем больше кривизна менисков, тоесть тем меньше радиус кривизны.
Искривление поверхности ведёт к смене поверхностного давления, уменьшая его при образовании вогнутого мениска. Так если погрузить трубку, диаметр которой достаточно мал для того, в ней мог образоваться мениск, а стенки которой хорошо смачиваются, в широкий сосуд с водой, то уровень воды в такой трубке подымится на некоторую высоту, по сравнению с уровнем воды в большом сосуде. Поднятие воды будет происходить до тех пор, пока разница поверхностных давлений не уравновесится разницей гидростатических давлений столбов воды в соединённых сосудах.
Капилляр с радиусом R погружен в большой сосуд с водой. Диаметр большого сосуда настолько большой, что поверхность воды в нём плоская. Вода подымается на высоту Н. Если R – радиус кривизны мениска капилляра, а Q – Угол смачивания, то
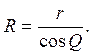 (4)
(4)
Допускаем, что капилляр имеет цилиндрическую форму, а мениск, отсюда, одинаковую кривизну во всех направлениях, тогда на основании формулы Лапласа получим:
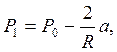 (5)
(5)
Где Р1 и Р0 – соответственно поверхностное давление в капилляре и сосуде с водой, А – поверхностное натяжение. Далее
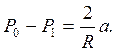 (6)
(6)
Эта разница и есть тем отрицательным давлением, которое образуется в следствие образовавшегося вогнутого мениска в трубке. Как мы уже отмечали выше, это отрицательное давление уравновешивает давление столбика воды в капилляре. Обозначив плотность воды через d, а гидростатическое давление, которое оказывает столбик воды на 1 см2, через Q, имеем
Q = Hdg дин/см2 , (7)
Где G – Ускорение силы притяжения.
Очевидно, что
P0 – P1 = Q. (8)
Отсюда,
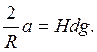 (9)
(9)
Так как
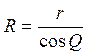 , (10)
, (10)
То
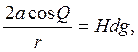 (11)
(11)
Откуда
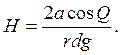 (6.15) (12)
(6.15) (12)
Обратите внимание:
— формула (12) даёт возможность определить поверхностное натяжение воды по высоте подъёма воды в капилляре и величину краевого угла между мениском жидкости и стенкой капилляра;
— высота подъёма воды в капилляре зависит только от радиуса капилляра: ![]() 1/2 (остальные величины в формуле постоянны).
1/2 (остальные величины в формуле постоянны).
При полном смачивании и плотности воды 1
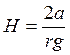
Где Н – высота поднятия воды в капилляре; а – поверхностное натяжение воды; r – радиус капилляра; q – ускорение силы притяжения.![]()
Таким образом, высота поднятия воды в капилляре обратно пропорциональна его радиусу (закон Жюрена).
Подставляем в только что приведённую формулу числовое значение q и а:
Q = 981 см/сек2, а = 74 дин/см;
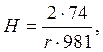 (14)
(14)
Откуда получили формулу Жюрена:
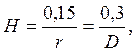 (15)
(15)
Где Н – высота капиллярного подъёма, см; r – радиус капилляра, мм; D – диаметр капилляра.
В очень тонких капиллярах поднятия жидкости может достигать большой высоты. Например, в капилляре диаметром 1 мкм вода (P = 103 кг/м3, а = 0,073 Н/м) при условии полного смачивания (Q = 0) поднимается на высоту
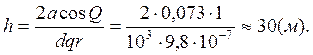 (16)
(16)
Таким образом, первопричиной капиллярного поднятия есть поверхностная энергия, присущая стенкам трубки. Эта энергия, расходуясь, вызывает искривление поверхности жидкости и соответствующее снижение поверхностного давления, вследствие которого происходит нарушение равновесия в системе, и вода поднимается в трубке до уровня, который определяется формулой Жюрена. После этого давление слоя воды, который прилегает к стенкам капилляра, заставляет поверхность мениска распространяться по стенкам трубки вверх, при чём на стенках образуется слой адсорбированной воды.
Таким образом мы рассмотрели случай, когда вода подымается и удерживается в капилляре, будучи соединенной с большим количеством воды в большом сосуде. В почве такое явление можно наблюдать в поведении капиллярно подпёртой воды.
Возникает вопрос, а как же будет удерживаться в почве капиллярно-подвешенная вода, когда выше и ниже смоченного слоя находятся сухие слои.
Представим себе такой пример. Изолированный цилиндрический капилляр, в который можно постепенно вводить воду сверху, причём образование пузырьков воздуха исключено.
В определённый начальный момент в капилляре образуется столбик воды небольшой высоты (рис 5.а). Рассмотрим условия равновесия этого столбика. Он будет находиться под влиянием трёх сил: силы веса Q, направленной вниз, поверхностного давления верхнего мениска Р1, направленного так же вниз, и поверхностного давления нижнего мениска Р2, направленного вверх.
Обозначим через H высоту столбика воды в сантиметрах, через D – её плотность и через R – радиус капилляра в сантиметрах. Масса столбика воды будет, очевидно, равна
![]() г, (17)
г, (17)
А давление Q, Которое развивается силой притяжения на 1см2, будет
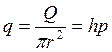 Г/см2, (18)
Г/см2, (18)
Или
![]() Дин/см2,
Дин/см2,
Q – ускорение силы тяжести, см/сек2.
Условия равновесия требуют, чтобы
![]() . (20)
. (20)
По формуле Лапласа, если капилляр имеет цилиндрическую форму, то
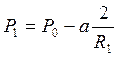 (21)
(21)
И
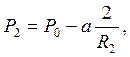 (22)
(22)
Где R1 и R2 – соответственно радиусы кривизны верхнего и нижнего менисков.
Подставляя эти выражения в предыдущее уравнение, получим:
(23)
Откуда 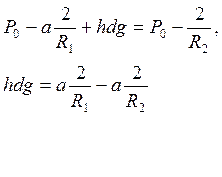 (24)
(24)
И 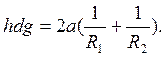 (25)
(25)
Таким образом мы доказали, что условием уравновешенного состояния такого столбика воды, как будто «висячего» в капилляре, есть различная кривизна верхнего и нижнего менисков. Так как левая половина последнего уравнения – величина положительная при всех условиях, положительной должна быть и правая половина.
Таким образом, ![]() >
> ![]() и R1 < R2, тоесть верхний мениск должен иметь меньший радиус кривизны и, отсюда, большую кривизну, чем нижний. Только при таких условиях поверхностное давление, которое образуется нижним мениском, будет большим, чем то, которое создаётся верхним, причём разница двух давлений, направленных снизу вверх, и уравновесит силу веса водного столбика, направленную вниз.
и R1 < R2, тоесть верхний мениск должен иметь меньший радиус кривизны и, отсюда, большую кривизну, чем нижний. Только при таких условиях поверхностное давление, которое образуется нижним мениском, будет большим, чем то, которое создаётся верхним, причём разница двух давлений, направленных снизу вверх, и уравновесит силу веса водного столбика, направленную вниз.
Обратимся к рисунку 5. Если будем продолжать вводить воду в наш капилляр, то с увеличением H водного столбика Hdg в уравнении 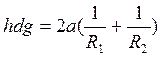 будет также возрастать. Вместе с тем условия равновесия требуют увеличения и правой части уравнения:
будет также возрастать. Вместе с тем условия равновесия требуют увеличения и правой части уравнения:
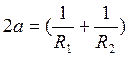 . В ней величина А постоянна;
. В ней величина А постоянна;
R1, тоесть радиус кривизны верхнего мениска, — так же величина постоянная и равна 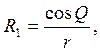 где Q – угол смачивания. Поэтому правая часть уравнения может увеличиваться только за счёт уменьшения величины
где Q – угол смачивания. Поэтому правая часть уравнения может увеличиваться только за счёт уменьшения величины ![]() и, таким образом, увеличения величины R2. Другими словами, кривизна нижнего мениска с увеличением высоты водного столбика будет уменьшаться, вследствие чего поверхностное натяжение нижнего мениска будет увеличиваться при постоянстве поверхностного давления верхнего мениска. Наконец наступит момент (рис. 5), когда нижний мениск станет плоским. В этот момент, очевидно,
и, таким образом, увеличения величины R2. Другими словами, кривизна нижнего мениска с увеличением высоты водного столбика будет уменьшаться, вследствие чего поверхностное натяжение нижнего мениска будет увеличиваться при постоянстве поверхностного давления верхнего мениска. Наконец наступит момент (рис. 5), когда нижний мениск станет плоским. В этот момент, очевидно,
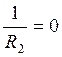 (26)
(26)
И
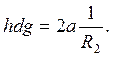 (27)
(27)
При дальнейшем увеличении нижний мениск примет уже выпуклую форму, и величина R2 станет в силу сложившихся условий положительной. Уравнение приобретает вид
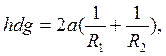
(28)
что отвечает случаям ![]() И
И ![]() На рисунке 5.
На рисунке 5.
Кривизна нижнего мениска будет увеличиваться до тех пор, пока капля, которая образуется в конце капилляра, не оторвётся и не упадёт вниз.
Приведённые примеры объясняют поведение воды в капиллярах, которые имеют форму трубки. Они дают возможность понять физическую сущность явления. В действительности почвенные капилляры имеют самую разнообразную форму, их диаметр по длине капилляра не постоянный. Так как таких случаев очень много и описание их заняло бы очень много места, то мы этого делать не будем, а отошлём читателя к специальной литературе (А. А. Роде, 1965; В. П. Гордієнко, 2008).