7.1. Задання та зображення багатогранникiв
Багатогранною поверхнею, або багатогранником, називають сукупнiсть кiнцевого числа плоских багатокутникiв, що не лежать в однiй площинi. Твiрнi багатокутники називають гранями, їхнi сторони ребрами, а вершини — вершинами багатогранника. Багатогранники можуть бути замкненими й незамкненими. Для незамкнених багатогранникiв (наприклад призм i гiрамiд) задання поверхнi й проекцiями зводять, як правило, до задания вiдсiку цiєї поверхнi. На рис. 7.1, а зображено призматичну поверхню, а на рис. 7.1, 6 багатогранний кут (пiрамiдальну поверхню), якi задано їхнiми ребрами.
Двi пiвплощини, що перетинаються, утворюють двогранний кут. Якщо в будь-якiй площi простору перетинасться бiльше нiж два плоских вiдсiки, то в результатi перетину утворюється багатогранний просторовий кут. Якщо всi гранi просторового кута лежать по один бiк вiд кожної його гранi, то такий кут називають опуклим. На рис. 7.2, а зображено чотиригранний кут.
Проте спосiб задания проекцiями ребер не єдиний. Так, пiрамiдальну поверхию можна задати i вершиною та плоскою ламаною, що не лежать у однiй площинi, або просторовою ламаною. Ламана є напрямною лiнiєю пiрамiдальної поверхнi. Призматичну поверхню можна утворити рухом прямої твiрної, напрямленої в невласну вершину поверхнi, що перетинає довiльну ламану напрямну, як плоску, так i просторову. Невласна вершина призматичної поверхнi може бути задана напрямом у
Просторi.
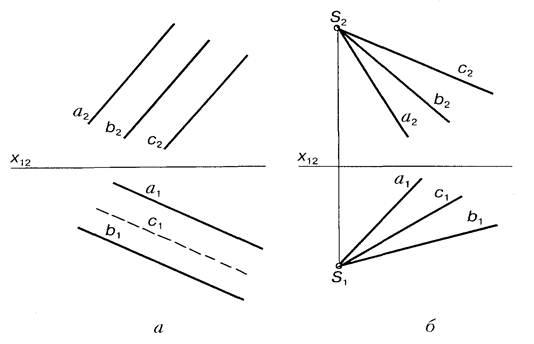
Рис. 7.1.
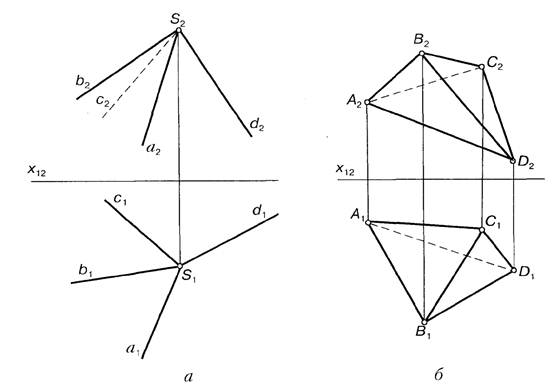
Рис. 7.2.
Якщо площини, що утворюють багатогранну поверхню, замкненi, то вони утворюють замкнений багатогранник (рис. 7.2, б). Сукупнiсть усiх ребер багатогранника називають його сiткою. Багатогранники повно та однозначно при непроекцiювальних гранях задають сiткою їнiх ребер. Багатогранник, розмiщений по один бiк вiд площини будь-якої його гранi, називають опуклим, у противному разi — неопуклим. Гранями опуклого багатогранника є опуклi багатокутники. Багатогранний кут при будь-якiй вершинi опуклого багатогранника також опуклий. Число граней Г, вершин В та ребер Р будьякого опуклого замкненого багатогранника визначають теоремою
Декарта — Ейлера:
Г+В-Р= 2.
Опуклий багатогранник можна також задати системою лiнiйних нерiвностей з трьома невiдомими:
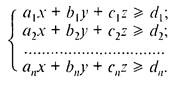
7.2. Правильнi багатогранники
Із множини багатогранникiв в окрему групу видiляють правильнi опуклi багатогранники, або тiла Платона. У таких багатогранникiв усi ребра, гранi, кути (плоскi, двограннi та просторовi) рiвнi мiж собою. Розрiзняють такі види правильних багатогранникiв:
т е т р а е др (чотиригранник), гранями якого с чотири рiвностороннiх трикутники (рис. 7.3, а). Побудову його доцiльно починати з горизонтально проекцiТ;
о к т а е д р (восьмигранник), гранями якого є вiсiм рiвностороннiх трикутникiв (рис. 7.3, 6). В окремому положеннi на двох проекцiях октаедр зображується квадратом з дiагоналями.
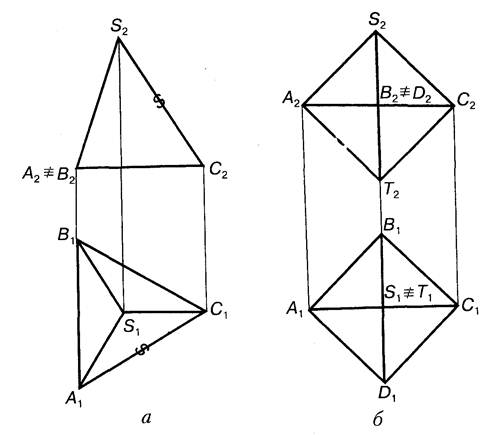
Рис. 7.3.
7.3. Пiрамiди, призми, призматоїди.
На практицi часто застосовують простi багатогранники. Багатогранник називають простим, якщо: а) всi його гранi є простими багатокутниками, тобто такими, в яких жодна пара несумiжних сторiн не мае спiльних точок; б) жоднi двi несумiжнi гранi не мають спiльних точок, крiм, може, спiльної вершини; в) двi сумiжнi гранi мають лише одне спiльне ребро i не мають iнших спiльних точок. Крiм правильних багатогранникiв широко застосовують також пiрамiди, призми та призматоїди.
Пiрамiда — це багатогранник, усi гранi якого. крiм однiєi, мають спiльну вершину, яку називають вершиною пiрамiди (рис. 7.4). Пiрамiду можна дiстати, якщо перетнути багатогранний кут площиною, яка не проходить через вершину кута i перетинає всi ребра цiє поверхнi. Оскiлькн всi бiчнi гранi пiрамiдни є трикутниками, пiрамiда цiлком визначається заданням її основи та вершини.
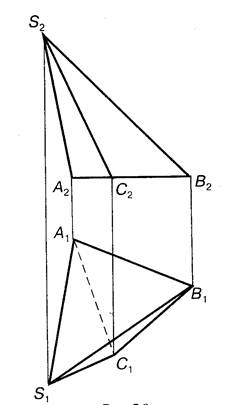
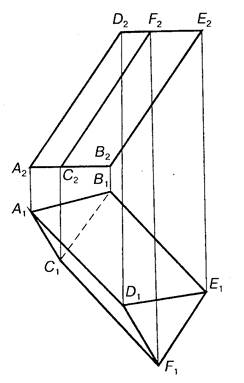
Рис. 7.4. Рис. 7.5.
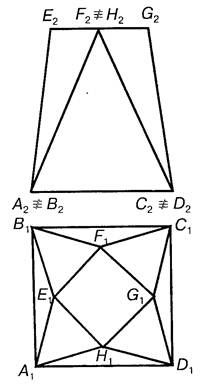
Рис. 7.6
Призмою називають багатогранник, обмежений призматичною поверхнею та двома паралельними площинами, якi не паралельнi ребрам призми (рис. 7.5.). Цi двi гранi називають основами призми, гранi призматичної поверхнi — бічними гранями, а її ребра ребрами призми.
Основами призми є рiвнi мiж собою багатокутники, бiчнi ребра призми дорiвнюють одне одному. Якщо основи не паралельнi мiж собою, то призма є зрiзаною. Якщо основами призми є перпендикулярнi перерiзи призматичної поверхнi, то призму називають прямою, у разi невиконання
Цiєї умови — похилою.
Призми та пiрамiди розрiзняють за числом кутiв основи. Якщо основою є правильний багатокутник, а висота збiгається з вiссю, то пiрамiду й призму називають правильними.
Призматоїд — це опуклий багатогранник, усi бiчнi гранi якого є трикутниками або трапецiями. Основи призматоїда паралельні одна однiй i є будь-якими багатокутниками. На рис. 7.6 зображено призматоїд, основами якого є квадрати АВСD та ЕFGН.
7.4. Перетин багатогранників з прямою та площиною
При перетині багатогранників прямою лінією можливі два випадки: 1) грані багатогранника проекціювальні; 2) грані багатогранника займають загальне положення. У першому випадку точки перетину прямої з гранями відразу визначають на одній з проекцій, а в другому — слід виконати ще додаткові побудови.
Нехай пряма загального положення l перетинає пряму трикутну призму АВС (рис. 7.7). Точки перетину 1 і 2 прямої з гранями визначають безпосередньо на полі П1. Фронтальні проекції їх визначають за вертикальною відповідністю. Відрізок між точками входу та виходу невидимий на обох проекціях.
Перетин прямої загального положення з похилою призмою зображено на рис. 7.8. При цьому доцільно застосувати косокутне проекціювання у напрямі ребер призми на площину її нижньої основи. Призма спроекціюється своєю основою, а пряма — відрізком А1 В2. Перетин допоміжної проекції прямої з основою визначить допоміжні проекції точок перетину прямої з гранями призми: точки |1 і 21. Зворотним про-екціюванням визначають горизонтальні проекції шуканих точок І1 і 2}. Фронтальні проекції визначають за вертикальною відповідністю.
Перстин прямої з поверхнею трикутної піраміди показано на рис. 7.9. Тут також застосовано допоміжне проекціювання, але не паралельне, а центральне з вершини піраміди S на горизонтальну площину її основи. При цьому піраміда спроекціюється своєю основою, а відрізок прямої — відрізком D1 Е1. У перетині з основою визначають допоміжні проекції шуканих точок 11 і 21, які також центральне повертаються напряму D1Е1. Це точки L1, і 21,. Фронтальні проекції визначають за вертикальною відповідністю або повертають оберненим центральним допоміжним проекціюванням на поле П2.
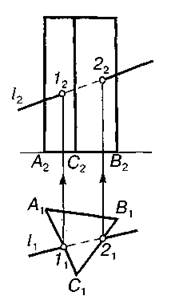
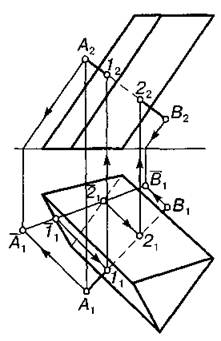
Рис.7.7 Рис.7.8
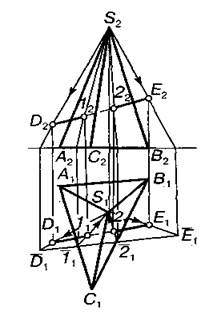
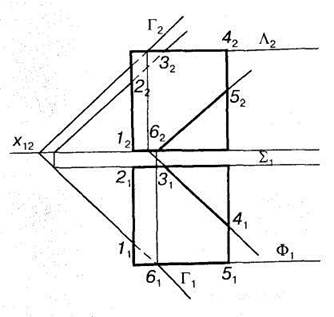
Рис.7.9. Рис.7.10.
Розглянемо перетин багатогранників і площини. Тут можливі чотири випадки:
1) багатогранник і січна площина перебувають у проекціювальному положенні;
2) багатогранник перебуває в загальному положенні, а площина — в проекціювальному;
3) багатогранник перебуває в проекціювальному положенні, а площина — в загальному;
4) багатогранник і січна площина перебувають у загальному положенні. На рис. 7.10 зображено куб, який перетинається з площиною загального положення Г, заданою слідами. В результаті перетину утворюється шестикутник 1—2—3—4―5—6—1, вершини якого визначають за допомогою проекціювальннх площин, що проходять через грані куба. Так визначено відрізок 3—4 за допомогою горизонтальної січної площини A, що проходить через верхню грань куба. Ця площина перетне площину Г по горизонталі, яка в перетині т горизонтальною основою куба визначає точки З і 4. Відрізок шестикутника перерізу 5—6 дістанемо за допомогою фронтальної площини Ф, а відрізок 2—3 — за допомогоюфронтальноїплощини ∑.
Якщо січна площина займає. загальне положення, а призма є трикутною, розміщеною вертикально, то горизонтальна проекція лінії перетину 1—2—3 збігається з горизонтальною проекцією призми (рис. 7.11) . При цьому слід визначити її фронтальну проекцію. Це можна зробити за дпомогою фронталей, проведених через вершини горизонтальної проекції призми, які в перетині з ребрами призми дадуть точки 12,22 і 32) На рис. 7.12 зображено похилу трикутну призму, яка перетинається фронтально проекціювальною площиною. Фронтальна проекція трикутника перерізу 12 2232 збігається з фронтальним слідом площини. Горизонтальна проекція перерізу визначена за допомогою вертикальної відповідності.
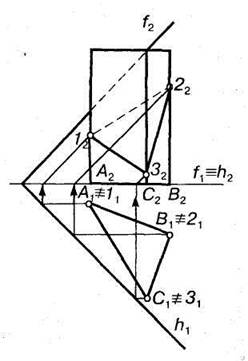
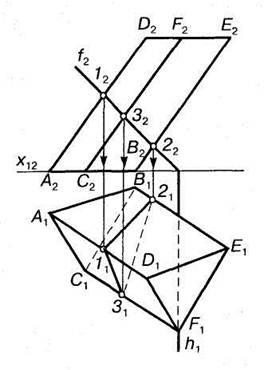
Рис.7.11. Рис.7.12.
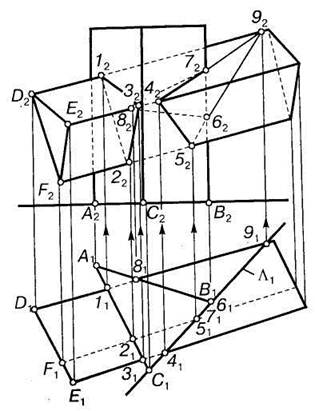
Рис. 7.13.
Список рекомендованої літератури
Гордон В. О., Семенцов-Огиевский М. А. Курс начертательной геометрии.- М.: Изд-во Наука, 1988. – 270 с.
Михайленко В. Є., Ковальов С. М. та ін. Нарисна геометрія. Підручник для вузів. – К.:Вища школа,1993. – 134с.
Винницкий И. Г. Начертательная геометрия. Учебник для вузов. – М.: Высшая школа, 1985.- 168с.
Михайленко В. Е. та ін. Инженерная графика. – Киев: Высшая школа, 1990.-290 с.
Михайленко В. Е. та ін. Інженерна та комп’ютерна графіка. За ред. Михайленка В. Е. Київ: Вища школа, 2000.