Цель занятия: Освоить методику решения оптимизационных задач при помощи средства поиска решения в MS Excel. Применить эту методику к решению задачи об оптимальном управлении капиталом.
План занятия:
Изучить постановку задачи об управлении портфелем активов.
Построить модель, описывающую данную задачу.
Решить задачу, используя средство подбора параметров.
Самостоятельно решить задачу управления активами с учетом возможных рыночных рисков.
Порядок выполнения работы
Рассмотрим задачу об управлении портфелем активов.
Пусть перед некоторым инвестором стоит проблема принятия решения о вложении имеющегося у него капитала. Набор характеристик потенциальных объектов для инвестирования, имеющих условные имена от А до F, задаются в таблице.
|
Название |
Доходность, в % |
Срок выкупа, год |
Надежность, баллы |
|
A |
5,5 |
2001 |
5 |
|
B |
6,0 |
2005 |
4 |
|
C |
8,0 |
2010 |
2 |
|
D |
7,5 |
2002 |
3 |
|
E |
5,5 |
2000 |
5 |
|
F |
7,0 |
2003 |
4 |
Предположим, что при принятии решения о приобретении активов должны быть соблюдены условия:
Суммарный объем капитала, который должен быть вложен, составляет $100 000.
Доля средств, вложенная в один объект, не может превышать четверти от всего объема.
Более половины всех средств должны быть вложены в долгосрочные активы (пусть к таковым относятся активы со сроком погашения после 2004 года).
Доля активов, имеющих надежность менее 4 баллов, не может превышать трети суммарного объема.
Опишем экономико-математическую модель данной задачи оптимизации. В качестве управляемых переменных выступают объемы средств, вложенных в активы той или иной фирмы. Обозначим их как XA, XB, XC , XD, XE, XF.
Тогда суммарная прибыль от размещенных активов, которую получит инвестор, может быть представлена в виде: P=0,055XA + 0,006XB + 0,08XC +0,075XD +0,055XE +0,07XF.
На следующем этапе моделирования необходимо формально описать перечисленные выше ограничения1 — 4 на структуру портфеля.
Ограничения на суммарный объем активов:
XA + XB + XC + XD + XE + XF <= 100 000
Ограничение на размер доли каждого актива:
XA <=25 000, XB <= 25 000, XC <= 25 000, XD <= 25 000, XE <= 25 000, XF <= 25 000
Ограничение, связанное с необходимостью вкладывать половину средств в долгосрочные активы:
XB + XC >= 50 000
Ограничение на долю ненадежных активов:
XC + XD <= 30 000
Система ограничений в соответствии с экономическим смыслом задачи должна быть дополнена условиями неотрицательности для искомых переменных:
XA >= 0, XB >= 0, XC >= 0, XD >= 0, XE >= 0, XF >= 0.
Перечисленные условия образуют математическую модель поведения инвестора. В рамках этой модели может быть поставлена задача поиска таких значений переменных XA, XB, XC, XD , XE, XF, при которых достигается наибольшее значение прибыли и одновременно выполняются ограничения на структуру портфеля активов.
Перейдем к решению сформулированной задачи с помощью MS Excel. Оно распадается на следующие шаги:
На рабочем листе задать ячейки, которые будут предназначены для сохранения переменных решаемой задачи (XA, XB, XC , XD, XE, XF).
Задать ячейку, содержащую формулу целевой функции Р (формулу см. выше) — ячейка Н2.
Заполнить ячейки для формул "сложных ограничений" (типа XC + XD <= 30 000). В нашем примере это ячейки С4, С5, С6.
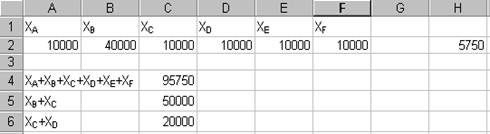
Выполнить команду Сервис® Поиск решения
Заполнить параметры диалогового окна следующим образом:
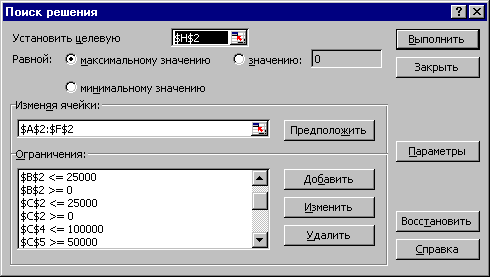
Ввод ограничений осуществляется при помощи кнопки Добавить. Аналогично можно изменять и удалять ограничения
После ввода всех ограничений и заполнения окна Поиск Решения нажать кнопку Выполнить, после чего будет осуществлена процедура поиска решения, удовлетворяющего всем ограничениям. По результатам выводится сообщение о найденном решении (или невозможности его обнаружить).
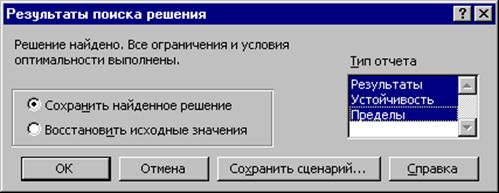
Полученные результаты можно сохранить, изменив таким образом содержимое ячеек (нажать ОК) или отказаться от сохранения результатов. Можно сформировать отчет с более подробной информацией о том, как происходил процесс решения. Для этого необходимо выбрать тип отчета.
После сохранения найденного решения, получим следующие результаты:
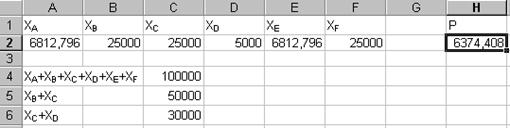
Таким образом, получили, что при оптимальном распределении прибыль инвестора составит 6374,408.
Задания для самостоятельной работы:
|
Фирма |
Процент |
Риск |
Ограничения |
Средневзвешенный риск не более 7% Общая сумма вклада 100000 руб. Повторить расчет модели при снятых ограничениях на минимальную сумму вклада. |
|
A |
30 |
90 |
<=10% |
|
|
B |
12 |
10 |
<=30% |
|
|
C |
7 |
2 |
<=50% |
|
|
D |
15 |
9 |
<=25% |
|
|
E |
9 |
3 |
<=50% |
|
|
Вариант 2 |
||||
|
Фирма |
Процент |
Риск |
Ограничения |
Средневзвешенный риск не более 5% Общая сумма вклада 100000 руб. Повторить расчет модели при снятых ограничениях на минимальную сумму вклада. |
|
A |
19 |
12 |
<=10% |
|
|
B |
18 |
10 |
<=30% |
|
|
C |
7 |
2 |
<=50% |
|
|
D |
15 |
7 |
<=25% |
|
|
E |
9 |
3 |
<=50% |
Средневзвешенный риск рассчитывается по формуле:
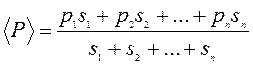 ,
,
Где p – риски соответствующих банков, s – сумма вклада в данный банк.
Контрольные вопросы:
Каковы составляющие модели оптимизации?
Что такое целевая функция?
В чем различие простых и сложных ограничений?
Как рассчитывается средневзвешенное значение?
Какую дополнительную информацию выдает средство поиска решения?