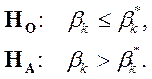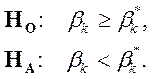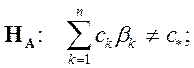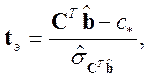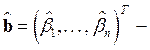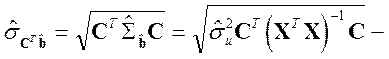ОЦЕНКА КАЧЕСТВА РЕГРЕССИОННЫХ КОЭФФИЦИЕНТОВ И ОТДЕЛЬНЫХ ЧАСТЕЙ РЕГРЕССИОННОЙ МОДЕЛИ

II. 1. t-критерий проверки гипотез об истинных, но неизвестных значениях отдельных или нескольких коэффициентов регрессии.

Используя t-критерий, исследователь желает статистически доказать, что эти коэффициенты Не равны определенному значению, сформулированному в качестве нулевой гипотезы, или, что истинные, но неизвестные значения нескольких коэффициентов уравнения Не удовлетворяют определенному соотношению величин. Доверительное оценивание, которое тесно связано с применением t-критерия, также может быть использовано для проверки гипотез о числовых значениях отдельных коэффициентов регрессии или их линейных комбинаций.

Условием проведения t-теста является во-первых, само наличие Классической регрессионной модели с выполнением Предпосылки относительно нормального распределения, что в свою очередь означает:

Вектор возмущений Является Мерным нормально распределенным вектором, с Нулевым вектором математического ожидания и Единичной Ковариационной матрицей ;

Регрессионная матрица Детерминирована и имеет полный ранг равный.

Общее для t-критерия является следующее утверждение о распределении: Случайная переменная

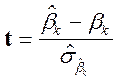(II.1)

Подчиняется центральному T-распределению с степенями свободы.

II. 2. t-критерий двусторонней пары гипотез.

В регрессионном анализе весьма важным является вопрос: Существенно ли влияет Й регрессор В генеральной совокупности на регрессанд, иными словами: Отличается ли истинное (но неизвестное) значение коэффициента регрессии от нуля?

При формулировке гипотез важным является то положение, которое обычно довольно часто рассматривается в каждом введении в теорию тестов и связано с понятиями: Ошибки первого рода (основная гипотеза отвергается, хотя она верна) и Ошибки второго рода (основная гипотеза не отвергается, хотя она не верна). Утверждение, которое статистически должно быть подтверждено тестом, формулируется как Альтернативная гипотеза.

Таким образом, мы подошли к моменту формулировки основной гипотезы:

(II.2)

И альтернативной гипотезы:

(II.3)

Рассчитанная по формуле:

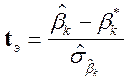(II.4)

В более общем случае есть любое, заранее установленное и логически обоснованное вещественное число[1] t-статистика является реализацией центрированной t-распределенной случайной величины с степенями свободы.

Основное правило принятия решений.

Гипотеза отклоняется, если (*) Где: Абсолютное значение t-статистики, рассчитанной по формуле (II.4); Табличное значение t-распределения (t-критерий) для уровня значимости и степеней свободы.

При этом для t-критерия имеет место следующее соотношение:

Эта величина, как известно, называется Квантилем t-распределения с степенями свободы.

Замечание: Так как при построении вероятность означает, что t-распределенная случайная переменная попадает в область принятия гипотезы, то, очевидно, что является вероятностью ошибки первого рода — Основная гипотеза отвергается, хотя она верна.

II. 3. t-критерий односторонней пары гипотез.

При необходимости проверки утверждения относительно того, превышает или нет параметр определенную величину должны быть сформулированы односторонние основные и альтернативные гипотезы, что выглядит следующим образом:

I.

II.

Область принятия гипотезы имеет теперь другие границы (см. таблицу).

№	Основная гипотеза	Альтернатив-ная гипотеза	Тест	Область принятия гипотезы	Область отклонения гипотезы
1			Двусто-ронний	Т. е.:	или Т. е.
2			Односто-ронний
3			Односто-ронний

II. 4. Проведение тестирования с помощью t-критерия и важный его, часто нарушаемый принцип.

Тестирование может быть проведено по следующей схеме, которая состоит из шести основных шагов:

Формирование пары гипотез и ;

Выбор уровня значимости ;

Получение соответствующего теоретического значения t-критерия из таблиц;

Получение расчетного (эмпирического) значения t-статистики;

Сравнение рассчитанной величины t-статистики с ее табличным значением и принятие решения об отклонении гипотезы;

Интерпретация результатов тестирования.

Замечание:

Важный принцип Проведения тестов состоит в том, что первый и второй шаги должны выполняться прежде, чем станут известны выборочные данные, используемые для оценки параметров. Исходные данные не должны получаться в результате пассивного наблюдения. Если какая-либо информация о выборочных данных учитывается при формировании рабочих гипотез или при выборе уровня значимости, возникает опасность искажения теста.

При проведении теста во многих случаях удобно пользоваться не фиксированным значением уровня значимости , а рассчитывать так называемый Эмпирический уровень значимости. Он и служит критерием принятия решения.

Продемонстрируем применение t-критерия на примере регрессии, рассмотренном в главе. Были получены следующие результаты оценивания методом 1МНК:

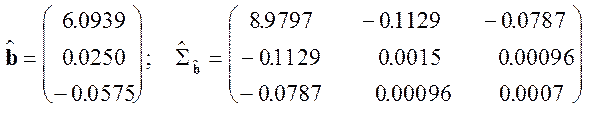
Осуществим проверку рабочей гипотезы, что второй регрессор в генеральной совокупности не оказывает существенного влияния.

Здесь .

Пусть

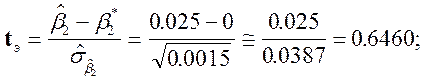
. Таким образом, гипотеза может быть принята как верная.

Так как основная гипотеза принимается, то оказывается возможным статистически доказать, что второй регрессор не оказывает существенного влияния на точность прогнозов. При этом необходимо было бы применить и другие критерии.

II. 5. t-тест гипотез о линейной комбинации коэффициентов регрессии.

В регрессионном анализе наибольший интерес представляет величина соотношений линейных комбинаций регрессионных коэффициентов. Предположим, что по некоторым соображениям, с целью упрощения модели, исследователь решается объединить целую группу регрессоров полученной ранее эмпирической функции регрессии под одним более общим (глобальным) признаком:

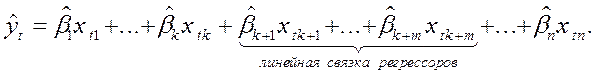
Тогда для линейной связки регрессоров:

Становится необходимым исследование возможных значений соответствующих линейных комбинаций оценок регрессионных коэффициентов

Здесь выше приведенная методика оценки в целом может быть сохранена, за исключением некоторых изменений.

В общем случае Нулевая и альтернативная гипотезы на примере Двустороннего T-теста Имеют вид[2]:

Нулевая гипотеза в полном виде: (II.5) Где Постоянные, значения которых задаются на основе теоретических соображений; Истинные неизвестные значения регрессионных коэффициентов; Скаляр, значение которого жестко задано на основе теоретических соображений (числовое значение линейной комбинации регрессионных коэффициентов, включенных в нулевую гипотезу — формула (II.5)). В матричном виде: (II.6) Где Наперед заданные постоянные; — вектор регрессионных коэффициентов.

Альтернативная гипотеза В полном виде: (II.7) В матричном виде: (II.8)

Односторонние гипотезы[3]:

Или

.

Формула для вычисления t-статистики в этом случае имеет следующий вид:

(II.9) Где Постоянные величины; Значение линейной комбинации согласно нулевой гипотезе; Оцененный методом 1МНК вектор регрессионных коэффициентов; Оцененная методом 1МНК стандартная ошибка линейной комбинации.

II. 6. Доверительные интервалы для отдельных коэффициентов и их линейных комбинаций.

Доверительный интервал, называемый также Интервальной оценкой, дает ценную информацию о надежности точечной оценки. Интервальная оценка лучше, чем точечная оценка, использует информацию, содержащуюся в моделях и данных.

Определение: Доверительный интервал для регрессионного коэффициента при уровне доверия является интервалом со случайно зависимыми границами; он включает (накрывает) истинное значение Го регрессионного коэффициента с вероятностью .

Как отмечено выше. В классической линейной модели нормальной регрессии случайная переменная

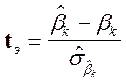
Является центрированной t-распределенной переменной с степенями свободы; и являются случайными переменными. Используя значение из таблиц t-распределений, получим:

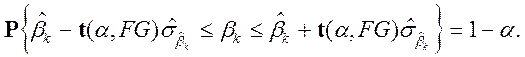(II.10)

Таким образом, двусторонний симметричный доверительный интервал имеет нижней границей величину: и верхней границей — величину . Аналогичным образом задаются границы двустороннего симметричного интервала с уровнем доверия для линейной комбинации : Нижняя граница и Верхняя граница.

Вывод формул других доверительных интервалов (особенно односторонних) осуществляется аналогично.

II. 7. F-критерий проверки гипотез о группах регрессионных коэффициентов и их линейных комбинациях.

F-тест, также как и T-тест относится к случаю линейной модели нормальной регрессии, однако применяется для проверки только двусторонних гипотез. Посредством F-теста могут быть статистически проверены гипотезы о значении Нескольких коэффициентов или нескольких линейных комбинаций, а также сочетаний того и другого. В этом отношении F-тест является более общим, чем T-тест.

Общая линейная гипотеза В классической линейной модели регрессии, проверяемая F-тестом имеет следующий вид:

(II.11)

(II.12)

Здесь:

вектор-столбец, состоящий из элементов ;

вектор-столбец регрессионных коэффициентов, подлежащих оцениванию;

Матрица размерности , где Количество линейных уравнений (линейных гипотез), которые в совокупности образуют группу нулевых и альтернативных гипотез, проверяемых F-тестом.

Входящее в нулевую гипотезу Е уравнение имеет вид

Совместность всех указанных уравнений (линейных гипотез) обеспечивается лишь в том случае, если ранг матрицы равен (то есть количество линейно независимых строк матрицы равен ).

Замечание: F-тест проверяет гипотезы, представляющие собой совокупность (группу) частных гипотез как единое целое. Если , F-тест приводит к аналогичным результатам, что и получаемые T-тестом. Однако это вовсе не означает что при можно F-тест заменить двусторонним T-тестом.

II. 8. F-статистика и правило применения F-теста.

Для проверки гипотез с помощью F-теста, необходимо вычислить эмпирическое значение F-статистики. Для этого используют формулу

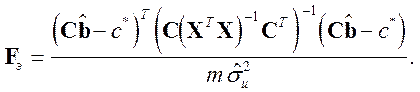(II.13)

В условиях классической линейной модели нормальной регрессии и справедливости нулевой гипотезы случайная переменная имеет F-распределение с степенями свободы, где

Таким образом, правило применения F-теста может быть сформулировано следующим образом:

отклоняется, если Где Соответствующий квантиль F-распределения (табличное значение , F-критерий).

II. 9. F-тест проверки гипотез для нескольких регрессионных коэффициентов.

Здесь с помощью F-теста проверяется, оказывают ли Последние регрессоров как группа Влияние на регрессанд. При этом значение может быть вычислено по следующей формуле

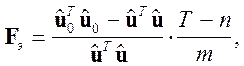(II.14)

Где Сумма квадратов ошибок в регрессии с регрессорами;

Сумма квадратов ошибок в регрессии, из которой исключена группа исследуемых регрессоров.

Таким образом, здесь осуществляются расчеты по двум регрессиям.

II. 10. F-тест проверки гипотез для одного регрессионного коэффициента или одной линейной комбинации.

В случае, когда , F-тест и двусторонний T-тест дают одинаковые результаты. Таким образом, в данном случае F—Статистика равна квадрату T—Статистики:

Для соответствующих табличных значений также верно соотношение

[1] Частный случай, когда , рассмотрен выше.

[2] Для удобства рассматривается линейная комбинация всех регрессионных коэффициентов модели.

[3] Также возможны, однако редко используются в экономических исследованиях.