Микро- и макропараметры состояния газа
Основное уравнение МКТ
Температура. Абсолютная температура
Уравнение Менделеева-Клапейрона
Связь температуры со средней кинетической энергией молекул вещества
Микро — и макропараметры состояния газа
Система, состоящая из большого числа молекул, называется макросистемой. Макросистема, отделенная от внешних тел стенками с постоянными свойствами, после длительного промежутка времени приходит в равновесное состояние. Это состояние можно описать рядом параметров, называемых Параметрами состояния. Различают Микропараметры и Макропараметры состояния.
К микропараметрам состояния можно отнести следующие физические величины: массу M0 молекул, их скорость, среднюю квадратичную скорость молекул, среднюю кинетическую энергию молекул, среднее время между соударениями молекул, длину их свободного пробега и др. Это такие параметры, которые можно отнести и к одной молекуле макросистемы.
Макропараметры состояния характеризуют только равновесную систему в целом. К ним относятся объем V, давление P, температура T, плотность , концентрация N, внутренняя энергия U, электрические, магнитные и оптические параметры. Значения этих параметров могут быть установлены с помощью измерительных приборов.
Молекулярно-кинетическая теория идеального газа устанавливает соответствие между микропараметрами и макропараметрами газа.
Таблица. Mикропараметры состояния
| Параметр | Обозначение | Единицы в СИ |
| Масса молекулы | M0 | Кг |
| Скорость молекулы | М/c | |
| Cредняя квадратичная скорость движения молекул | М/c | |
| Средняя кинетическая энергия поступательного движения | Дж |
Таблица. Макропараметры состояния
| Параметр | Обозначение | Единицы в СИ | Способ измерения (косвенный способ) |
| Масса газа | M | Кг | Весы |
| Объем сосуда | V | М3 | Мерный цилиндр с водой; измерение размеров и расчет по формулам геометрии |
| Давление | P | Па | Манометр |
| Температура | T | К | Термометр |
| Плотность | | Кг/м3 | Измерение массы, объема и расчет |
| Концентрация | N | 1/м3 = м-3 | Измерение плотности и расчет с учетом молярной массы |
| Cостав (молярная масса и соотношение количеств ) | М1, М2,
1: 2 |
Кг/моль
безразмерная |
Приготовление газа смешением заданных масс или объемов |
Основное уравнение молекулярно-кинетической теории идеального газа
Это уравнение связывает макропараметры системы – давление P и концентрацию молекул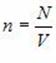 С ее микропараметрами – массой молекул, их средним квадратом скорости или средней кинетической энергией:
С ее микропараметрами – массой молекул, их средним квадратом скорости или средней кинетической энергией:
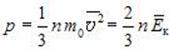
Вывод этого уравнения основан на представлениях о том, что молекулы идеального газа подчиняются законам классической механики, а давление – это отношение усредненной по времени силы, с которой молекулы бьют по стенке, к площади стенки.
Пропорциональность силы, с которой молекулы воздействуют на стенку, их концентрации, массе и скорости каждой молекулы качественно понятны. Квадратичный рост давления со скоростью связан с тем, что от скорости зависит не только сила отдельного удара, но и частота соударений молекул со стенкой.
Учитывая связь между концентрацией молекул в газе и его плотностью ( = Nm0), можно получить еще одну форму основного уравнения МКТ идеального газа:
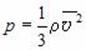
Температура. Абсолютная температура
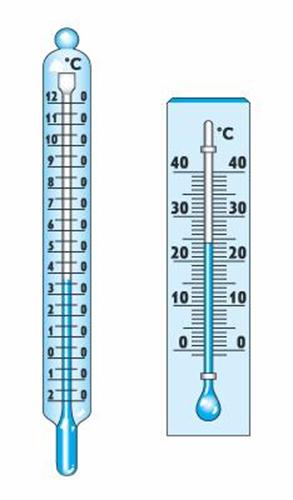
Рис. 2. Жидкостные термометры
При контакте двух макросистем, каждая из которых находится в равновесии, например, при открывании крана между двумя теплоизолированными сосудами с газом или контакте их через теплопроводящую стенку, равновесие нарушается. Через большой промежуток времени в частях объединенной системы устанавливаются новые значения параметров системы. Если говорить только о макропараметрах, то выравниваются температуры тел.
Понятие «температура» было введено в физику в качестве физической величины, характеризующей степень нагретости тела не по субъективным ощущениям экспериментатора, а на основании объективных показаний физических приборов.
Термометр – прибор для измерения температуры, действие которого основано на взаимно-однозначной связи наблюдаемого параметра системы (давления, объема, электропроводности, яркости свечения и т. д.) с температурой (рис. 2).
Считается, что если этот вторичный параметр (например, объем ртути в ртутном термометре) при длительном контакте с одним телом и при длительном контакте с другим телом одинаков, то это значит, что равны температуры этих двух тел. В экспериментах по установлению распределения молекул по скоростям было показано, что это распределение зависит только от степени нагретости тела, измеряемой термометром. В современной статистической физике характер распределения частиц системы по энергиям характеризует ее температуру.
Для калибровки термометра необходимы тела, температура которых считается неизменной и воспроизводимой. Обычно это температура равновесной системы лед – вода при нормальном давлении (0 °С) и температура кипения воды при нормальном давлении (100 °С).
В СИ температура выражается в кельвинах (К). По этой шкале 0 °С = 273,15 К и 100 °С = 373,15 К. В обиходе используются и другие температурные шкалы.

Уравнение Менделеева – Клапейрона (уравнение состояния идеального газа)
В результате экспериментальных исследований многих ученых было установлено, что макропараметры реальных газов не могут изменяться независимо. Они связаны уравнением состояния:
PV = vRT
Где R = 8,31 Дж/(K·моль) – универсальная газовая постоянная, 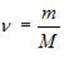 , где M – масса газа и M – молярная масса газа. Уравнение Менделеева – Клапейрона называют Уравнением состояния, поскольку оно связывает функциональной зависимостью Параметры состояния. Его записывают и в других видах:
, где M – масса газа и M – молярная масса газа. Уравнение Менделеева – Клапейрона называют Уравнением состояния, поскольку оно связывает функциональной зависимостью Параметры состояния. Его записывают и в других видах:
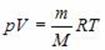
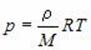
Пользуясь уравнением состояния, можно выразить один параметр через другой и построить график первого из них, как функции второго.
Графики зависимости одного параметра от другого, построенные при фиксированных температуре, объеме и давлении, называют соответственно Изотермой, Изохорой и Изобарой.
Например, зависимость давления P от температуры T при постоянном объеме V и постоянной массе M газа – это функция 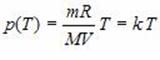 , где K – постоянный числовой множитель. Графиком такой функции в координатах P, Т будет прямая, идущая от начала координат, как и графиком функции Y(x)=kx в координатах Y, x (рис. 3).
, где K – постоянный числовой множитель. Графиком такой функции в координатах P, Т будет прямая, идущая от начала координат, как и графиком функции Y(x)=kx в координатах Y, x (рис. 3).
Зависимость давления P от объема V при постоянной массе M газа и температуре T выражается так:
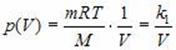 ,
,
Где K1 – постоянный числовой множитель. График функции 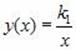 В координатах Y, x представляет собой гиперболу, так же как и график функции
В координатах Y, x представляет собой гиперболу, так же как и график функции ![]() В координатах P, V.
В координатах P, V.
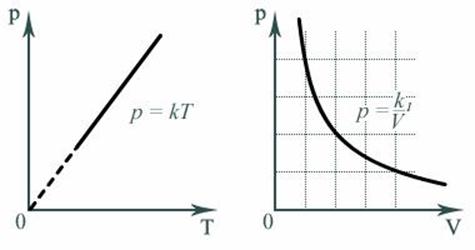
Рис. 3
Связь температуры со средней кинетической энергией молекул вещества
Количественное соотношение между температурой T (макропараметром) системы и средней кинетической энергией ![]() (микропараметром) молекулы идеального газа может быть выведено из сопоставления основного уравнения МКТ идеального газа
(микропараметром) молекулы идеального газа может быть выведено из сопоставления основного уравнения МКТ идеального газа 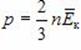 И уравнения состояния
И уравнения состояния 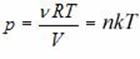 , где
, где 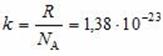 Дж/К – постоянная Больцмана. Сопоставляя два выражения для давления, получим
Дж/К – постоянная Больцмана. Сопоставляя два выражения для давления, получим
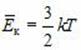
Средняя кинетическая энергия молекул идеального газа пропорциональна температуре газа. Если молекулы газа образованы двумя, тремя и т. д. атомами, то доказывается, что это выражение связывает только энергию поступательного движения молекулы в целом и температуру.
С учетом этого соотношения на уровне микро — и макропараметров макросистемы можно утверждать, что в Состоянии теплового равновесия двух систем выравниваются температуры и в случае идеального газа средние кинетические энергии молекул.