Тема Моделювання економічного ризику на базі концепції теорії гри.

Концепція теорії гри

Задача 1. Фірма ставить за мету вихід на міжнародний ринок зі своєю продукцією. ЇЇ фахівцями опрацьовано чотири варіанти рішень , щодо випуску продукції. Маркетингові обстеження та опрацювання одержаної інформації показали, що рішення залежить від попиту (стану економічного середовища), який може бути представлений трьома варіантами . На базі застосування відповідних економіко-математичних (імітаційних) моделей розрахований функціонал оцінювання (прибуток у тис. грн.), який приведено в таблиці

Варіанти рішень	Варіанти станів середовища
	2,0	3,0	1,5
	7,5	2,0	3,5
	2,5	8,0	2,5
	8,0	5,0	4,5

Відомо також, що стан середовища може реалізуватися з імовірністю , з імовірністю , а з імовірністю . З іншого боку фірма впевнена у тому, що зіштовхнеться з конкурентами. Керівництво фірми вважає, що врахувати вплив конкуренції необхідно з вагою .

Необхідно обрати один з чотирьох варіантів рішення, який був би оптимальним:

А) згідно з критерієм Вальда;

Б) згідно з критерієм Севіджа;

В) згідно з критерієм Байєса;

Г) згідно з критерієм Ходжеса-Лемана.

Побудувати множину і ламану Ходжеса-Лемана.

Розв’язання. Перше, що спадає на думку, це застосувати критерій Вальда, що дає гарантований результат, з урахуванням антагоністичних інтересів середовища, але є надто консервативним, або ж обрати критерій Севіджа, що дозволяє одержати мінімаксну оцінку ризику щодо невикористання своїх можливостей (п’ята інформаційна ситуація ).

1.  Маємо: ; .

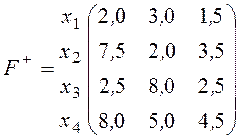
За критерієм Вальда, спочатку визначаємо найменший елемент у кожному рядку функціоналу оцінювання і далі, серед цих найменших елементів знаходимо найбільший:

,

,

,

,

.

Тобто, згідно з критерієм Вальда, оптимальним для нашого прикладу є рішення Х4.

Для обґрунтування прийняття рішення за критерієм Севіджа обчислимо матрицю невикористаних можливостей. Спочатку відшукаємо величини ,

,

,

.

Тепер обчислимо матрицю невикористаних можливостей:

Варіанти рішень	Варіанти станів середовища
	6,0	5,0	3,0
	0,5	6,0	1,0
	5,5	0,0	2,0
	0,0	3,0	0,0

Обчислимо

, ,

, .

Оптимальний розв’язок одержимо, знайшовши мінімальне із значень :

Отже, згідно з критерієм Севіджа, оптимальним для нашого прикладу є рішення , що в даному випадку співпадає з рішенням, одержаним за критерієм Вальда.

3. З другого боку, нам відомий розподіл апріорних імовірностей на елементах множини , тобто маємо інформацію, що є характерною для першої інформаційної ситуації . Для обґрунтування прийняття рішення можна керуватися критерієм Байєса. Згідно з критерієм при оптимальним є той розв’язок , що задовольняє умові:

.

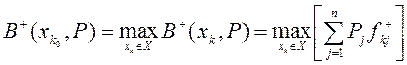У нашому випадку:

Отримуємо, що : .

Отже оптимальним розв’язком згідно критерію Байєса є .

4. Ми маємо апріорний розподіл імовірностей на станах економічного середовища. Керівництво фірми вважає, що має місце шоста інформаційна ситуація, як проміжна між першою та п’ятою при виборі середовищем своїх станів

Для неї критерієм обґрунтування прийняття рішень можна обрати скажімо критерій Ходжеса-Лемана:

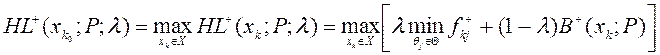
Маємо сукупність лінійних функцій :

,

,

,

.

Графіки цих функцій відображено на рисунку 2.2.2:

Бачимо, що прямі та розміщені на цьому малюнку нижче від прямих та . Отже, рішення та налалі до уваги можна не приймати.

Знайдемо точку з умови:

.

За умовою задачі , а для цих значень виконується нерівність . Отже, оптимальним за критерієм Ходжеса-Лемана є рішення для якого

.

Для рішення множину Ходжеса-Лемана стосовно параметра l складає відрізок [0; 0,07]. Для рішення — . Для рішень та Множини Ходжеса-Лемана є пустими.

Ламаною Ходжеса-Лемана є лінія АВС на рис. 2.2.2.

Задача 2. Припустимо, що підприємство випускає певну продукцію партіями фіксованого розміру. Через випадкові збої у виробничому процесі можливий випуск партій з недопустимо високим відсотком бракованої продукції. Визначають стани економічного середовища: — придатна партія виробів, — бракована партія виробів.

Нехай браковані вироби у придатній партії складають 4%, а в непридатній – 15%. Проведені на підприємстві розрахунки показують, що ймовірність виробництва бракованої партії дорівнює 0,2, а, відповідно, ймовірність придатної для відправки споживачам партії дорівнює 0,8. Таким чином і Підприємство відправляє партії двом споживачам А та Б.

За контрактом відсоток бракованих деталей, які відправляються споживачам А та Б, не повинен перевищувати 5 та 8% відповідно. За один відсоток перевищення встановлених меж браку передбачається штраф у розмірі 100 ум. од. З іншого боку, виробництво партії товарів більш високої якості збільшує затрати підприємства на 80 ум. од. за кожен відсоток. У задачі існують два варіанти рішень (дві альтернативи): — відправити партію споживачеві А, — відправити партію товарів споживачеві Б.

Припустимо, що підприємець вирішує перевірити два вироби з усієї партії. В результаті перевірки може бути встановлено, що: 1) обидва вироби придатні; 2) один з виробів придатний; 3) обидва вироби браковані.

Підприємець повинен прийняти рішення щодо того, кому із споживачів А чи Б відправляти певну партію виробів з урахуванням результатів перевірки.

Розв’язання. Функціонал оцінювання у цій ситуації доцільно подати у вигляді матриці витрат (в ум. од.): .

Якщо виробник приймає рішення , то у випадку придатної партії виробів () він матиме збитки: (5-4)×80=80 (ум. од.); у випадку бракованої партії виробів () штраф складе: (15-5)×100=1000 (ум. од.).

Якщо виробник приймає рішення , то у випадку придатної партії виробів () він матиме збитки: (8-4)×80=320 (ум. од.); у випадку бракованої партії виробів () штраф складе: (15-8)×100=700 (ум. од.).

Отже маємо

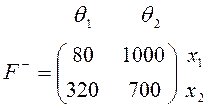
Зазначимо, що коли підприємець хоче обрати рішення за критерієм Вальда (принципом гарантованого результату), то він повинен відправити партію виробів споживачеві Б. (Перевірте).

Коли ж підприємець приймає рішення, користуючись наявною інформацією щодо та то згідно з критерієм Байєса, партію виробів доцільно відправляти споживачеві А. (Перевірте).

Розглянемо як зміниться рішення підприємця залежно від результатів перевірки двох виробів з партії.

Позначимо через x — випадкову величину кількості придатних виробів серед двох перевірених. Ця величина може приймати три значення: . Необхідно визначити умовні ймовірності , які використовуються при обчисленні апостеріорних імовірностей станів економічного середовища . Тобто, потрібно обчислити імовірність вироблення придатної чи бракованої партії, враховуючи результати експерименту . Наведемо загальну формулу для обчислення апостеріорних ймовірностей на основі апріорних ймовірностей та умовних імовірностей , якщо і :

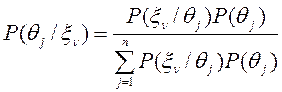
Ці ймовірності відомі як Байєсівські ймовірності.

У нашій задачі браковані вироби у придатній партії складають 4%, а в непридатній партії – 15%. Використовуючи біноміальний закон розподілу можна обчислити значення умовних імовірностей подій залежно від якості партії виробів:

, ,

, ,

, .

Знаходимо тепер апостеріорні ймовірності:

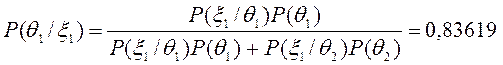
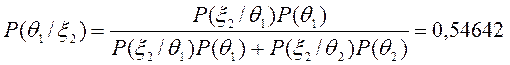
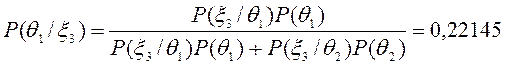
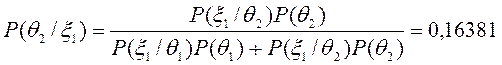
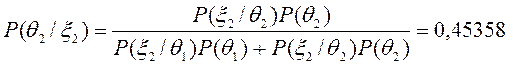
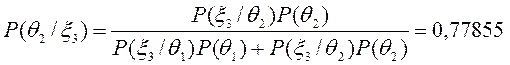
Остаточне рішення залежить від результатів контрольної перевірки

Згідно з критерієм Байєса загальна формула для підрахунку умовних сподіваних затрат має вигляд

,

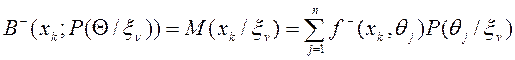Де — умовні імовірності, , .

Згідно умови задачі

Випадок 1. Обидва вироби придатні :

(ум од.).

(ум. од).

Мінімум умовних сподіваних значень досягається при . Отже, у цьому випадку рішення полягає у відправленні партії товарів споживачеві А, бо за критерієм Байєса рішення гарантує менші умовні сподівані витрати.

Випадок 2. Один з двох виробів є придатним:

(ум. од.)

(ум. од.)

Рішення полягає у відправленні партії товарів споживачеві Б : за критерієм Байєса забезпечує менші умовні сподівані витрати.

Випадок 3. Обидва вироби браковані:

(ум. од.)

(ум. од.)

Оскільки мінімум сподіваних значень затрат за критерієм Байєса досягається при , то рішення підприємця полягає у відправленні продукції споживачеві Б.

Навчальні задачі

1. Фермер планує засіяти взяту ним в оренду на короткий період (до 3-х років) земельну площу одною з сільськогосподарських культур: житом, вівсом, пшеницею чи гречкою. Оцінивши стан ґрунту цієї площі, фермер дійшов висновку, що отримання прибутку буде залежати в більшій мірі від погодних умов та закупівельних цін.

Запланований прибуток у млн. грн. та фактори, що на нього впливають, наведено в таблиці

№ п/п	Ціни, погодніУмовиКультура	Високі закуп. ціни та сприятливі погодні умови	Високі закуп. ціни та несприятливі погодні умови	Низькі закуп. ціни та сприятливі погодні умови	Низькі закуп. ціни та несприятливіПогодні умови
1.	Жито	15	10	9	7
2.	Овес	19	13	8	6
3.	Пшениця	20	12	12	4
4.	Гречка	21	15	10	4

Необхідно вибрати оптимальний варіант, якщо:

А) відомий розподіл ймовірностей ; ; ; ;}= {0,2; 0,2; 0,3; 0,3};

Б) розподіл ймовірностей невідомий, але відомо, що

;

В) розподіл ймовірностей невідомий;

Г) відомо, що на ринку сільгосппродукції наявна гостра конкуренція.

2. Нехай функціонал оцінювання відображає обсяги виручки, що її може отримати банк від реалізації акцій чотирьох компаній залежно від станів економічного середовища (у млн грн.)

Варіантрішення	Стани економічного середовища
Q1	Q2	Q3
Х1	6,0	6,2	5,5
Х2	7,5	7,1	7,0
Х3	7,4	7,5	8,0
Х4	7,0	5,8	6,0

Відомо, що стани економічного середовища можуть реалізуватись, відповідно, з ймовірностями: Р1 = 0,3; Р2 = 0,5; Р3 = 0,2.

Оберіть оптимальне рішення згідно з критеріями:

А) мінімальної семіваріації;

Б) мінімального коефіцієнта семіваріації.

3. Виходячи з умови Завдання 7, А також враховуючи, що ймовірності станів економічного середовища задовольняють умови Р2 > Р1 + Р3; Р3 > Р1, знайдіть оптимальне рішення, виходячи з критеріїв:

А) мінімальної дисперсії;

Б) мінімального коефіцієнта варіації.

4. Нехай функціонал оцінювання відображає обсяги виручки, що її може отримати банк від реалізації акцій чотирьох компаній залежно від станів економічного середовища (у млн грн.)

Варіантрішення	Стани економічного середовища
Q1	Q2	Q3	Q4	Q5
Х1	6,0	6,2	5,5	5,4	5,0
Х2	7,5	7,1	7,0	6,8	6,0
Х3	7,4	7,5	8,0	7,7	5,0
Х4	7,0	5,8	6,0	6,2	6,4

Відомо, що стани економічного середовища можуть реалізуватись, відповідно, з ймовірностями: Р1 = 0,1; Р2 = 0,3; Р3 = 0,4, Р4 = 0,15; Р5 = 0,05.

Оберіть оптимальне рішення за допомогою критеріїв:

А) Байєса;

Б) критерію мінімального сподіваного значення несприятливих відхилень.

5. Власник автозаправної станції прийняв рішення про надання додаткових послуг своїм клієнтам. Певну суму грошових коштів він може витратити на організацію:

—  продажу засобів догляду за автомобілем

—  продажу дрібних запчастин до автомобіля ;

—  продажу газетно-журнальної продукції ;

Рішення власника залежить від попиту на ті чи інші товари, який може характеризуватись станом:

—  попит на засоби догляду за автомобілем перевищує попит на запчастини і попит на газети і журнали ;

—  з трьох названих груп товарів переважає попит на запчастини ;

—  найбільшим є попит на газетно-журнальну продукцію ;

Виходячи зі свого досвіду, власник склав таблицю можливих прибутків залежно від можливого стану попиту на той чи інший товар.

Варіанти рішення	Варіанти попиту
	6,0	3,5	0,5
	6,5	7	4,0
	3,5	3,5	8,5

Обрати стратегію розвитку для АЗС.

6. Використавши дані задачі 3 знайти оптимальне рішення за критеріями, що відповідають першій інформаційній ситуації, якщо власнику автозаправної станції відомі оцінки ймовірностей можливих станів економічного середовища (попиту):

; ;

7. У зв’язку з переходом заводу на виготовлення нового виду продукції спеціалісти розробили п’ять варіантів рішень. Стан економічного середовища визначається рівнем забезпеченості матеріальними ресурсами. Спеціалісти виділяють три різні стани. Варіанти прибутку, що залежить від пари “рішення – стан економічного середовища” приведені в таблиці (тис. грн.).

Варіанти рішення	Стан економічного середовища
	2,5	3,5	4,0
	1,5	2,0	3,5
	3,5	8,0	2,5
	7,5	1,5	3,5
	8,5	1,5	4,0

Знайти варіант, який буде оптимальним для заводу з точки зору мінімуму ризику невикористаних можливостей.

8. Вибір фірми, що здатна стати партнером в сумісному підприємництві для машинобудівного підприємства, пов’язаний, в першу чергу, з визначенням технічних можливостей співробітництва. Відсутність у вітчизняного підприємства значних фінансових резервів у ВКВ зумовлює необхідність залучення зарубіжних партнерів, що є метою створення виробництва, яке стане конкурентноздатним на зовнішньому ринку, або такого, що замінює імпорт за умови повної валютної самоокупності. Керівництво підприємства повинне зробити вибір однієї з пропозицій зарубіжних фірм:

— фірма-партнер пропонує все основне технологічне обладнання (станки, преси тощо);

— компанія надає право на промислову власність (торгову марку і ліцензії);

— фірма передає інструменти, додаткове обладнання, “ноу-хау”;

— компанія приймає участь тільки в наданні грошових засобів в ВКВ.

На продукцію підприємства може бути: великий попит; середній попит; низький попит.

Виходячи з цього, керівництву підприємства була надана матриця прибутків(тис. дол.):

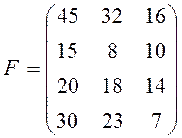
Керівництво підприємства цікавить така пропозиція зарубіжних фірм, яка дає можливість отримати як максимальний сподіваний прибуток, так і мати мінімальний ризик. Знайти компромісне рішення, скориставшись модифікованим критерієм, побудувати ламану, що відповідає оптимальному рішенню при .

9. Відділ маркетингу інноваційної фірми розробляє систему просування нового товару. Була розрахована матриця сподіваних доходів фірми за умов використання різних систем просунення товару при таких прогнозних ситуаціях на ринку аналогічних товарів: — попит перебільшує пропозицію; — пропозиція перебільшує попит; — попит співпадає з пропозицією; — попит на товари досить низький.

Ймовірності настання таких ситуацій на ринку невідомі, але прогнозується, що конкуренції на ринку не буде. Матриця сподіваних доходів наступна:

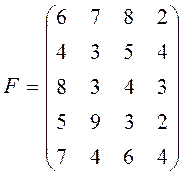
Необхідно вибрати оптимальну систему просування товарів, що забезпечує фірмі:

А) максимальний доход від продажу товарів;

Б) мінімальний ризик.

10. Приватна крамниця має 1000 одиниць нерозпроданих товарів літнього сезону. Попит на товар коливається в залежності від стану економічного середовища, причому — висока еластичність попиту, — низька еластичність попиту. Власник крамниці оцінює три варіанти рішень: — знизити ціну на 20%, — знизити на 30%, — на 40%.

За високої цінової еластичності зниження ціни на 20% дає змогу продати 700 одиниць товару, на 30% — 800 одиниць, на 40% — 900 одиниць; а за низької, знизивши ціну на 20%, сподіваються продати 400 од., на 30% — 500 од., на 40% — 600 од.

Собівартість товару становить 30$ за од., середня ціна (до її зниження) – 50$ . Еластичність попиту залежить від характеру літа: — жарке літо, — холодне літо. Різниця між собівартістю нерозпроданих товарів та виручкою, одержаної після продажу їх за зниженими цінами утворює функціонал збитків.

Експерти визначили ймовірності:

1)  настання жаркого літа – 0,6, настання холодного літа – 0,4;

2)  еластичності попиту на даний товар в наступному сезоні залежно від характеру літа:

=0,7; = 0,3; = 0,4; ) = 0,6;

Який з варіантів зниження ціни повинен вибирати власник крамниці, щоб збитки були мінімальними?

11. Підприємство випускає продукцію партіями фіксованого розміру. Через випадкові збої у виробничому процесі можливий випуск партій з недопустимо високим відсотком бракованої продукції. Визначено стани економічного середовища: партія виробів придатна; партія виробів непридатна.

Вважається, що браковані вироби у придатній партії становлять 3%, а в непридатній – 10%. Проведені розрахунки показують, що ймовірність виготовлення браку дорівнює 0,1. Підприємство відправляє партії товарів двом споживачам: А та В.

Контрактом обумовлено, що відсоток бракованої продукції, яка відправляється споживачам А та В, не повинен перевищувати, відповідно, 4% та 8%. За один відсоток перевищення встановлених меж передбачається штраф обсягом 5.000$. Водночас виробництво партії товарів вищої якості збільшує затрати підприємства на 4.000$ за кожен відсоток.

Керівництво підприємства розглядає два варіанти рішень (дві альтернативи): відправити партію товарів споживачеві А; відправити цю партію споживачеві В.

Підприємець вирішив перевірити три вироби з готової партії. В результаті перевірки виявилось, що серед взятих на перевірку трьох виробів придатними є два, а непридатним один.

Кому зі споживачів – А чи В підприємцеві доцільно відправити цю партію продукції?

12. При переході на випуск нових видів продукції опрацьовані три варіанти рішення Результати вибору залежать від невизначеного економічного середовища (від ціни на електроенергію та газ), яке може набувати чотири стани: . Відомий також функціонал оцінювання, що представляє собою затрати на виробництво продукції (тис. грн.):

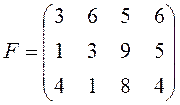
Відомі також ймовірності станів економічного середовища: ; ; ; .

Відшукати найкраще рішення згідно з критеріями: Ходжеса — Лемана, модифікованими..

13. При переході на випуск нових видів продукції опрацьовані три варіанти рішення Результати вибору залежать від невизначеного економічного середовища (від ціни на електроенергію та газ), яке може набувати чотири стани: .

Відомий функціонал оцінювання, що представляє собою матрицю прибутків від виробництва продукції (млрд. гр.):

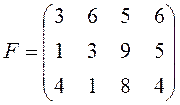
Група експертів вважає, що поведінка економічного середовища найкращим чином враховується зваженою комбінацією найкращого (з коефіцієнтом 0,4) та найгіршого (з коефіцієнтом 0,6).

Відшукати оптимальне рішення.

14. Фірма ставить за мету вихід на міжнародний ринок зі своєю продукцією. Її фахівцями опрацьовано три варіанти рішень щодо випуску продукції. Встановлено, що рішення залежить від попиту який може бути чотирьох варіантів: Обчислено функціонал оцінювання (прибуток у млн. грн.):

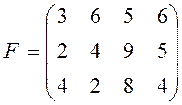
Відомі також ймовірності станів економічного середовища:

; ; ; .

Водночас керівництво фірми впевнене, що зіштовхнеться з конкурентами і воно вважає за потрібне врахувати вплив конкуренції з вагою

Вибрати оптимальне рішення.

15. Фірма ставить за мету вихід на міжнародний ринок зі своєю продукцією. Її фахівцями опрацьовано три варіанти рішень щодо випуску продукції. Побудовано функціонал оцінювання (прибуток у млн. грн.):

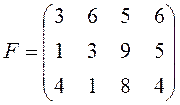
Фахівцями фірми також вважають, що для ймовірностей станів економічного середовища справедливі співвідношення:

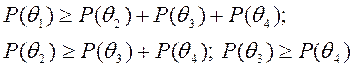
За знайденими оцінками ймовірностей станів економічного середовища, відшукати оптимальне рішення.