Кинематикой называется раздел теоретической механики, изучающий движение объектов (точек, тел), не зависящее от причин, обусловленных это движение.
Основными понятиями кинематики являются системы координат и время, а также движущиеся объекты — точки и тела. Точка в кинематике считается геометрической (не имеющая размеров); телом называется система точек, подчиненных некоторым связям. Если связи можно считать жесткими, то моделью реального тела является абсолютно твердое тело.
В качестве координат в кинематике используются системы ортогональные, трехмерные в пространстве и двумерные в плоскости. Могут использоваться сферическая (пространственная) и полярная (плоская) системы. Выбор системы координат определяется условиями задачи.
Основной задачей кинематики является аналитическое описание движения объекта.
Движение тела считается замкнутым, если для любого момента времени известно (или может быть определено) положение любой его точки. Поэтому изучение движения точки является первой задачей кинематики.
Три способа задания положения точки.
Линия, которую описывает точка при своем движении, называется траекторией. Если траекторией точки является прямая линия — то движение прямолинейное, если кривая — криволинейное.
Движение точки можно определить тремя способами: векторным, координатным и естественным.
Векторный способ:
Положение точки можно определить с помощью радиус-вектора ![]() , проведенного из неподвижной точки О в точку М.
, проведенного из неподвижной точки О в точку М.
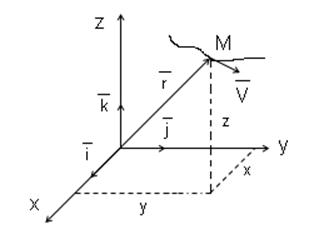
В данном случае функцией времени является
![]() (1)
(1)
— кинематическое уравнение движения точки в векторной форме.
Кривую, которую описывает точка М, называют годографом радиус-вектора ![]() .
.
Координатный способ задания движения:
В этом случае координаты точки задаются как функции времени:
![]() (2)
(2)
Между векторным и координатным способами существует связь:
![]() (3),
(3),
Где ![]() — единичные векторы(орты).
— единичные векторы(орты).
Если из уравнений (2) исключить параметр t, то получим уравнение траектории в явной форме.
Движение точки может быт задано в полярных координатах:
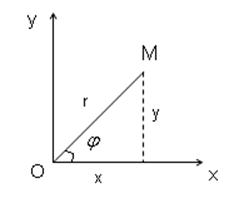
![]() ,
,
Где r — полярный радиус, ![]() — угол между полярным радиусом и полярной осью.
— угол между полярным радиусом и полярной осью.
Исключив параметр, t получим:
![]()
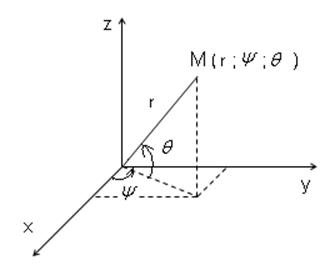
В трехмерном пространстве применяют цилиндрические и сферические координаты. Уравнения в цилиндрических координатах имеют вид:
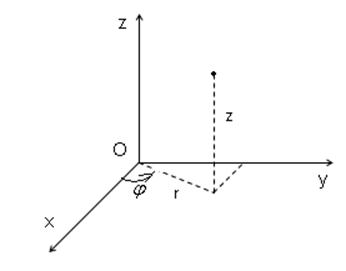
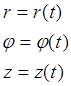
В сферических координатах положение точки определяется полярным радиусом r, углом ![]() и углом
и углом ![]() (полюсный угол):
(полюсный угол):
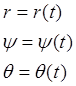
Естественный способ:
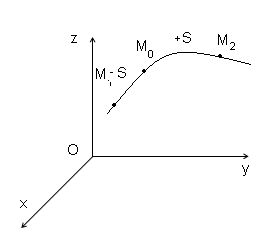
Закон движения точки описывается одним уравнением:
![]()
Скорость точки.
Прямолинейное движение.
![]() — для равномерного прямолинейного движения.
— для равномерного прямолинейного движения.
Из этой формулы можно записать:
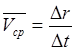 — скорость является физической величиной, определяющей перемещение точки за единицу времени.
— скорость является физической величиной, определяющей перемещение точки за единицу времени.
Криволинейное движение.
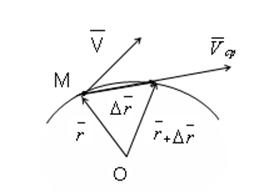
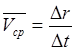
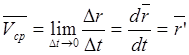
![]() (4)
(4)
Скорость точки равна первой производной радиус-вектора точки по времени (м/с).
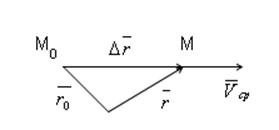
Скорость точки в некоторый момент времени t называется физическая величина, зависящая от t и позволяющая приближенно определить перемещение ![]() за достаточно малый промежуток времени как результат прямолинейного и равномерного движения.
за достаточно малый промежуток времени как результат прямолинейного и равномерного движения.
Скорость точки в прямоугольной декартовой системе координат.
Пусть ![]()
В этом случае скорость определяется по проекциям на оси координат, тогда:
![]() ;
; ![]()
Скорость по определению:
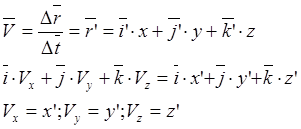
![]() или
или ![]()
Скорость точки при естественном способе задания движения.
При этом движение задано ![]() соответствует определенный радиус-вектор, который можно рассмотреть как:
соответствует определенный радиус-вектор, который можно рассмотреть как:
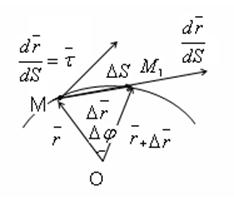
![]() ,
,
Поэтому скорость можно представить:
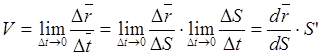
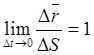 , т. к при
, т. к при ![]() ,
, ![]() , тогда
, тогда 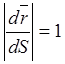 , предельное положение секущей
, предельное положение секущей ![]() — есть касательная к кривой, тогда
— есть касательная к кривой, тогда 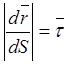 .
.
Тогда для этого случая заданная скорость будет равна:
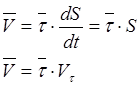
![]() — проекция скорости на касательную к траектории.
— проекция скорости на касательную к траектории.
Ускорение точки.
Ускорением точки в рассматриваемой системе координат называется мера изменения скорости точки, равная производной по времени от скорости этой точки.
Рассмотрим два положения точки:
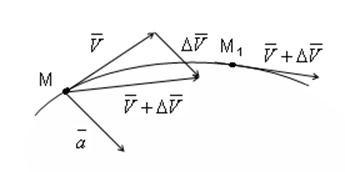
Отношение 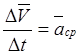 — среднее ускорение.
— среднее ускорение.
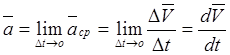
Так как ![]() , то:
, то:
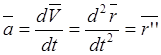
А [![]() ]
]
2. Ускорение при координатном способе задания.
![]()
![]()
![]()
![]()
![]()
![]()
![]() или
или ![]()
![]()
3. Ускорение точки при естественном способе задания.
Полное ускорение точки равно векторной сумме касательного (тангенсального) и нормального ускорений.
![]()
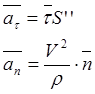 ,
,
Где ![]() — единичные орты
— единичные орты
![]() — радиус кривизны траектории.
— радиус кривизны траектории.
Модуль полного ускорения определяем:
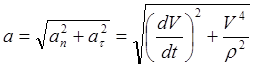
Если движение точки задано координатным способом, то можно получить следующие выражения:
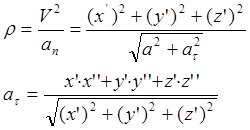
Простейшие движения твердого тела.
Поступательное движение тела.
Поступательным называется такое движение тела, при котором произвольная прямая, проведенная в теле, движется параллельно самой себе.
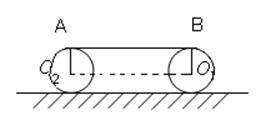
При поступательном движении тела все точки движутся с одинаковыми скоростями и ускорениями.
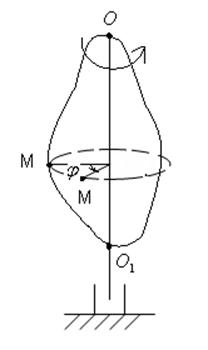
Вращательное движение вокруг неподвижной оси.
Вращательным движением тела вокруг неподвижной оси называется такое движение, при котором прямая, проходящая через какие-нибудь две точки О и ![]() во время движения тела остается неподвижной и называется
во время движения тела остается неподвижной и называется ![]() — осью вращения.
— осью вращения.
![]() — кинематическое уравнение вращательного движения вокруг неподвижной оси.
— кинематическое уравнение вращательного движения вокруг неподвижной оси.
Угловая скорость ![]() :
:
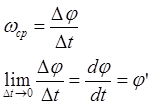
[![]() ]
]
Связь:
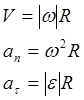
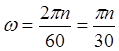 — связь угловой скорости с частотой вращения n
— связь угловой скорости с частотой вращения n
Угловое ускорение ![]() в данный момент времени равно первой производной по времени от угловой скорости или второй производной по времени от
в данный момент времени равно первой производной по времени от угловой скорости или второй производной по времени от ![]() :
:
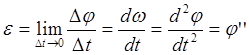 [
[![]() ]
]
Сложное движение точки.
Часто приходится исследовать движение точки относительно двух и более систем координат, из которых одна совершает движение относительно другой, условно принимаемой за неподвижную. В этом случае движении точки М относительно неподвижной системы координат ![]() называется абсолютным, а по отношению к подвижной системы координат
называется абсолютным, а по отношению к подвижной системы координат ![]() — относительным.
— относительным.
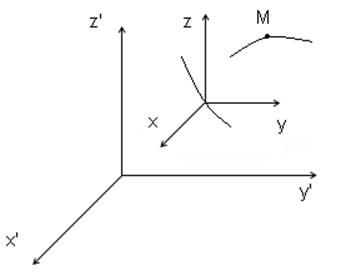
Движение подвижной системы координат ![]() относительно неподвижной
относительно неподвижной ![]() называется переносным. Основной задачей сложного движения точки является установление зависимости между кинематическими характеристиками абсолютного, переносного и относительного движений.
называется переносным. Основной задачей сложного движения точки является установление зависимости между кинематическими характеристиками абсолютного, переносного и относительного движений.
Скорость при сложном движении точки.
Абсолютная скорость ![]() точки при сложном движении точки равна векторной сумме относительной
точки при сложном движении точки равна векторной сумме относительной ![]() и переносной
и переносной ![]() скоростей:
скоростей:
![]()
Модуль абсолютной скорости:
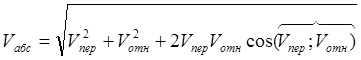
Ускорение.
Абсолютное ускорение точки при сложном движении равно векторной сумме относительного, переносного ускорений и ускорения Корнолиса:
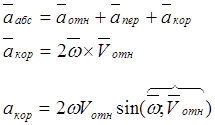
Правило определения направления вектора ускорения Корнолиса: для этого необходимо спроектировать вектор относительной скорости в плоскость, перпендикулярную оси вращения, и повернуть полученную проекцию на ![]() по направлению угловой скорости
по направлению угловой скорости ![]() .
.
Плоскопараллельное движение твердого тела.
Плоскопараллельным, или плоским, движением твердого тела называется такое движение, при котором все точки его движутся параллельно некоторой неподвижной плоскости.
При этом движении скорость любой точки М плоской фигуры геометрически складывается из скоростей полюса О и скорости точки М при вращении плоской фигуры вокруг полюса О.
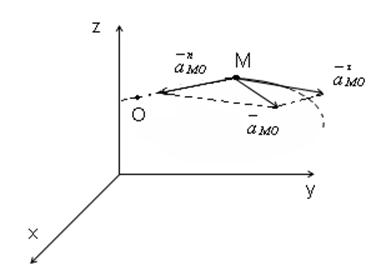
![]()
Ускорение аналогично:
![]()
Мгновенный центр скоростей (МЦС).
Мгновенным центром скоростей называется точка плоской фигуры, скорость которой в данный момент времени равна нулю.
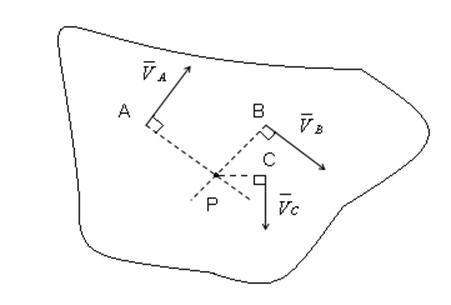
Для определения МЦС необходима провести перпендикуляры к вектором скоростей данных точек.
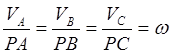
Частные случаи:
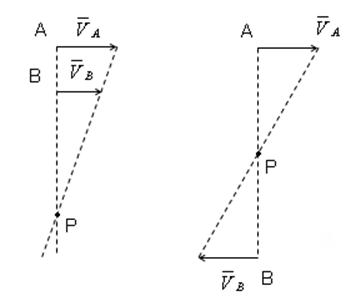
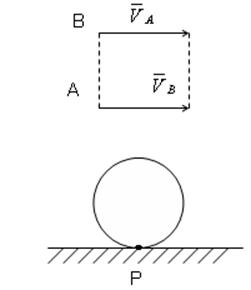
Мгновенный центр ускорений (МЦУ).
Мгновенным центром ускорений называется точка плоской фигуры, ускорение которой в данный момент времени равно нулю.
Ускорения любых точек плоской фигуры образуют в каждый момент времени один и тот же угол ![]() с отрезками, соединяющими эти точки с мгновенным центром ускорений.
с отрезками, соединяющими эти точки с мгновенным центром ускорений.
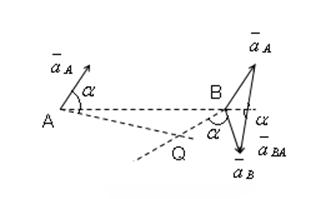
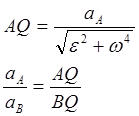
![]() — мгновенный центр ускорений.
— мгновенный центр ускорений.