Методы расчета электрических цепей постоянного тока

Изложение методов расчета и анализа электрических цепей, как правило, сводится к нахождению токов ветвей при известных значениях ЭДС и сопротивлений.

Рассматриваемые здесь методы расчета и анализа электрических цепей постоянного тока пригодны и для цепей переменного тока.

2.1 Метод эквивалентных сопротивлений

(метод свертывания и развертывания цепи).

Этот метод применяется только для электрических цепей содержащих один источник питания. Для расчета, отдельные участки схемы, содержащие последовательные или параллельные ветви, упрощают, заменяя их эквивалентными сопротивлениями. Таким образом, цепь свертывается до одного эквивалентного сопротивления цепи подключенного к источнику питания.

Затем определяется ток ветви, содержащий ЭДС, и схема разворачивается в обратном порядке. При этом вычисляются падения напряжений участков и токи ветвей. Так, например, на схеме 2.1 А Сопротивления R3 и R4 включены последовательно. Эти два сопротивления можно заменить одним, эквивалентным

R3,4=R3+R4

После такой замены получается более простая схема(Рис.2.1Б).

Здесь следует обратить внимание на возможные ошибки в определении способа соединений сопротивлений. Например сопротивления R1 и R3 нельзя считать соединенными последовательно, также как сопротивления R2 и R4 нельзя считать соединенными параллельно, т. к. это не соответствует основным признакам последовательного и параллельного соединения.

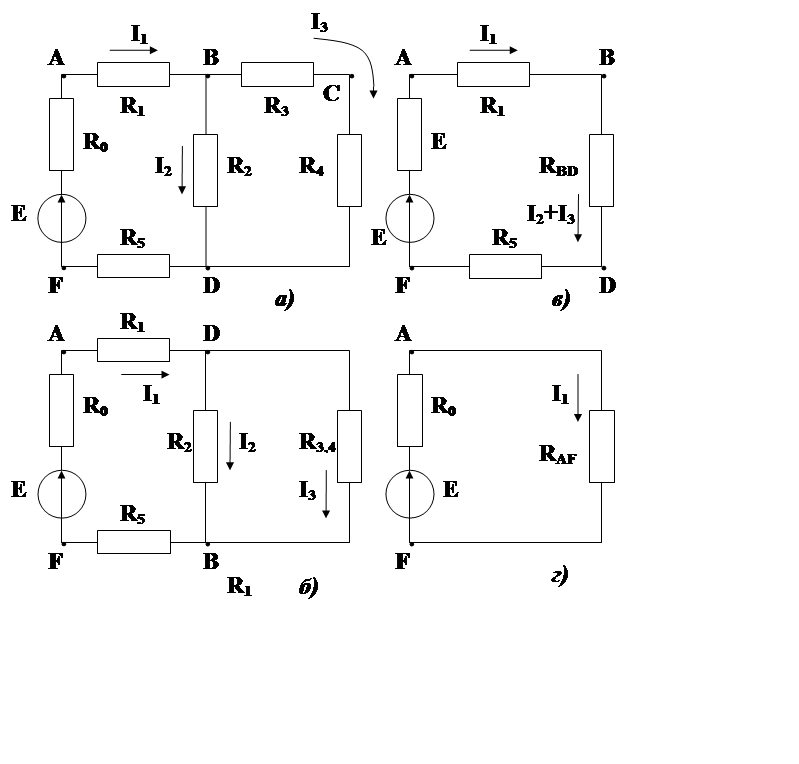Рис 2.1 К расчету электрической цепи методом

Эквивалентных сопротивлений.

Между сопротивлениями R1 и R2, в точке В, имеется ответвление с током I2.поэтому ток I1 Не будет равен току I3, таким образом сопротивления R1 и R3 нельзя считать включенными последовательно. Сопротивления R2 и R4 с одной стороны присоединены к общей точке D, а с другой стороны — к разным точкам В и С. Следовательно, напряжение, приложенное к сопротивлению R2 и R4 Нельзя считать включенными параллельно.

После замены сопротивлений R3 и R4 эквивалентным сопротивлением R3,4 и упрощением схемы (Рис. 2.1 Б), более наглядно видно, что сопротивления R2 и R3,4 соединены параллельно и их можно заменить одним эквивалентным, исходя из того, что при параллельном соединении ветвей общая проводимость равна сумме проводимостей ветвей:

GBD=G2+G3,4 , Или 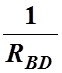=+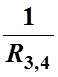Откуда

RBD=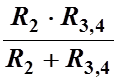

И получить еще более простую схему (Рис 2.1,В). В ней сопротивления R1, RBD, R5 соединены последовательно. Заменив эти сопротивления одним, эквивалентным сопротивлением между точками A и F, получим простейшую схему (Рис 2.1, Г):

RAF= R1 + RBD+ R5 .

В полученной схеме можно определить ток в цепи:

I1=.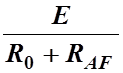

Токи в других ветвях нетрудно определить переходя от схемы к схеме в обратном порядке. Из схемы на рисунке 2.1 В Можно определить падение напряжения на участке B,D цепи:

UBD=I1·RBD

Зная падение напряжения на участке между точками B и D можно вычислить токи I2 и I3 :

I2= 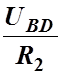, I3=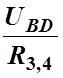

Пример 1. Пусть (Рис 2.1 А) R0 = 1 Ом; R1=5 Ом; R2=2 Ом; R3=2 Ом; R4=3 Ом; R5=4 Ом; Е=20 В. Найти токи ветвей, составить баланс мощностей.

Эквивалентное сопротивление R3,4 Равно сумме сопротивлений R3 и R4:

R3,4= R3 + R4=2+3=5 Ом

После замены (Рис 2.1 Б ) вычислим эквивалентное сопротивление двух параллельных ветвей R2 и R3,4:

RBD= 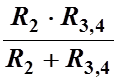==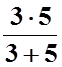1,875 Ом,

И схема еще упростится (Рис 2.1 В).

Вычислим эквивалентное сопротивление всей цепи:

RЭкв= R0+ R1+ RBD+ R5=11,875 Ом.

Теперь можно вычислить общий ток цепи, т. е. вырабатываемый источником энергии:

I1=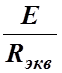 =1,68 А.

Падение напряжения на участке BD будет равно:

UBD= I1· RBD=1,68·1,875=3,15 В.

Развернув цепь дальше (Рис. 2.1 б) вычислим токи I2 и I3 :

I2=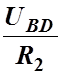==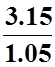1,05 А; I3=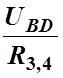==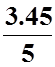0,63 А

Составим баланс мощностей:

Е· I1= I12·(R0+ R1+ R5) + I22· R2+ I32· R3,4 ,

20·1,68=1,682·10+1,052·3+0,632·5 ,

33,6=28,22+3,31+1,98 ,

33,6≈33,51

Минимальное расхождение обусловлено округлением при вычислении токов.

В некоторых схемах нельзя выделить сопротивлений включенных между собой последовательно или параллельно. В таких случаях лучше воспользоваться другими универсальными методами, которые можно применить для расчета электрических цепей любой сложности и конфигурации.

2.2 Метод законов Кирхгофа.

Классическим методом расчета сложных электрических цепей является непосредственное применение законов Кирхгофа. Все остальные методы расчета электрических цепей исходят из этих фундаментальных законов электротехники.

Рассмотрим применение законов Кирхгофа для определения токов сложной цепи (Рис 2.2) если ее ЭДС и сопротивления заданы.

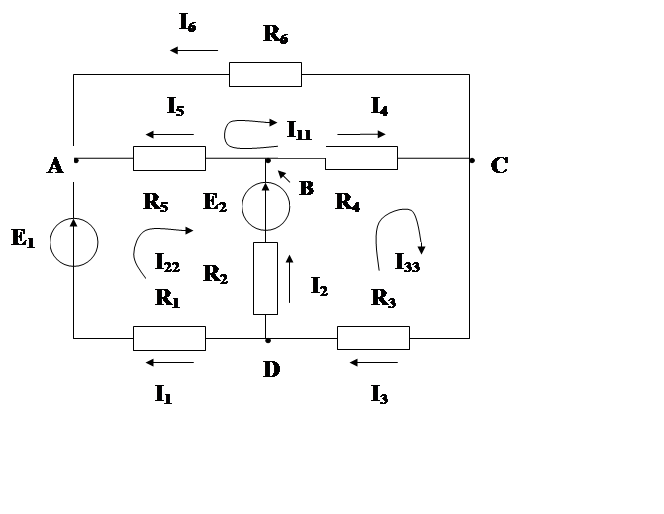
Рис. 2.2. К расчету сложной электрической цепи для

Определения токов по законам Кирхгофа.

Число независимых токов схемы равно числу ветвей (в нашем случае m=6). Поэтому для решения задачи необходимо составить систему из шести независимых уравнений, совместно по первому и второму законам Кирхгофа.

Количество независимых уравнений составленных по первому закону Кирхгофа всегда на единицу меньше чем узлов, Т. к. признаком независимости является наличие в каждом уравнении хотя бы одного нового тока.

Так как число ветвей M всегда больше, чем узлов К, То недостающее количество уравнений составляется по второму закону Кирхгофа для замкнутых независимых контуров,Т. е. чтобы в каждое новое уравнение входила хотя бы одна новая ветвь.

В нашем примере количество узлов равно четырем – A,B,C,D, следовательно, составим только три уравнения по первому закону Кирхгофа, для любых трех узлов:

Для узла A: I1+I5+I6=0

Для узла B: I2+I4+I5=0

Для узла C: I4+I3+I6=0

По второму закону Кирхгофа нам нужно составить также три уравнения:

Для контура A,C,В, А: I5·R5— I6·R6— I4·R4=0

Для контура D,A,В,D: I1·R1— I5·R5— I2·R2=Е1-Е2

Для контура D,В, С,D: I2·R2+ I4·R4+I3·R3=Е2

Решая систему из шести уравнений можно найти токи всех участков схемы.

Если при решении этих уравнений токи отдельных ветвей получатся отрицательными, то это будет указывать, что действительное направление токов противоположно произвольно выбранному направлению, но величина тока будет правильной.

Уточним теперь порядок расчета:

1)  произвольно выбрать и нанести на схему положительные направления токов ветвей;

2)  составить систему уравнений по первому закону Кирхгофа – количество уравнений на единицу меньше чем узлов;

3)  произвольно выбрать направление обхода независимых контуров и составить систему уравнений по второму закону Кирхгофа;

4)  решить общую систему уравнений, вычислить токи, и, в случае получения отрицательных результатов, изменить направления этих токов.

Пример 2. Пусть в нашем случае (рис. 2.2.) R6= ∞, что равносильно обрыву этого участка цепи (рис. 2.3). Определим токи ветвей оставшейся цепи. вычислим баланс мощностей, если E1=5 В, E2=15B, R1=3 Ом, R2 =5 Ом, R 3=4 Ом, R 4=2 Ом, R 5 =3 Ом.

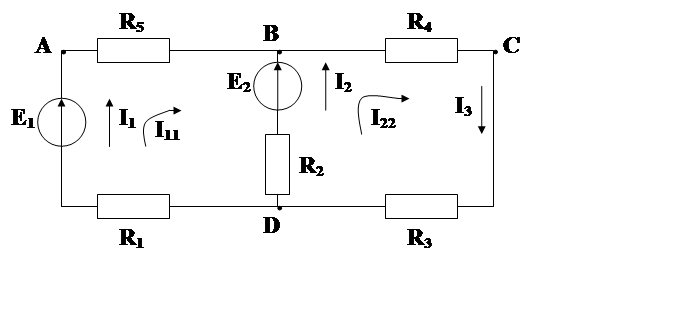
Рис. 2.3 Схема к решению задачи.

Решение. 1. Выберем произвольно направление токов ветвей, их у нас три: I1, I2, I3.

2. Составим только одно независимое уравнение по первому закону Кирхгофа, т. к. в схеме лишь два узла В и D.

Для узла В: I1+I2—I3=О

3. Выберем независимые контуры и направление их обхода. Пусть контуры ДАВД и ДВСД будем обходить по часовой стрелке:

E1-E2=I1(R1 + R5) — I2·R2,

E2=I2·R2 + I3·(R3 + R4).

Подставим значения сопротивлений и ЭДС.

I1+I2—I3=0

I1+(3+3)- I2·5=5-15

I2·5+I3(4+2)=15

Решив систему уравнений, вычислим токи ветвей.

I1=-0,365А; I2= I22— I11=1,536А; I3=1,198А.

Как проверку правильности решения составим баланс мощностей.

ΣEiIi= ΣIy2·Ry

E1·I1 + E2·I2 = I12·(R1 + R5) + I22·R2 + I32·(R3 + R4);

5(-0,365) + 15·1,536 = (-0,365)2·6 + 1,5632·5 + 1,1982·6

-1,82 + 23,44 = 0,96 + 12,20 + 8,60

21,62 ≈ 21,78.

Расхождения незначительны, следовательно решение верно.

Одним из главных недостатков этого метода является большое количество уравнений в системе. Более экономичным при вычислительной работе является Метод контурных токов.

2.3 Метод контурных токов.

При расчете Методом контурных токов полагают, что в каждом независимом контуре течет свой (условный) Контурный ток. Уравнения составляют относительно контурных токов по второму закону Кирхгофа. Таким образом количество уравнений равно количеству независимых контуров.

Реальные токи ветвей определяют как алгебраическую сумму контурных токов каждой ветви.

Рассмотрим, например, схему рис. 2.2. Разобьем ее на три независимых контура: СВАС; АВDА; ВСDВ и условимся, что по каждому из них проходит свой контурный ток, соответственно I11, I22, I33. Направление этих токов выберем во всех контурах одинаковым по часовой стрелке, как показано на рисунке.

Сопоставляя контурные токи ветвей, можно установить, что по внешним ветвям реальные токи равны контурным, а по внутренним ветвям они равны сумме или разности контурных токов:

I1 = I22, I2 = I33 — I22, I3 = I33,

I4 = I33 — I11, I5 = I11 — I22, I6 = — I11.

Следовательно, по известным контурным токам схемы легко можно определить действительные токи ее ветвей.

Для определения контурных токов данной схемы достаточно составить только три уравнения для каждого независимого контура.

Составляя уравнения для каждого контура необходимо учесть влияние соседних контуров токов на смежные ветви:

I11(R5 + R6 + R4) — I22·R5 — I33·R4 = O,

I22(R1 + R2 + R5) — I11·R5 — I33·R2 = E1 — E2,

I33(R2 + R3 + R4) — I11·R4 —I22·R2 = E2.

Итак, порядок расчета методом контурных токов выполняется в следующей последовательности:

1.  установить независимые контуры и выбрать направления в них контурных токов;

2.  обозначить токи ветвей и произвольно дать им направления;

3.  установить связь действительных токов ветвей и контурных токов;

4.  составить систему уравнений по второму закону Кирхгофа для контурных токов;

5.  решить систему уравнений, найти контурные токи и определить действительные токи ветвей.

Пример 3. Решим задачу (пример 2) методом контурных токов, исходные данные те же.

1.  В задаче возможны только два независимых контура: выберем контуры АВDА и ВСDВ, и примем направления контурных токов в них I11 и I22 по часовой стрелке (рис. 2.3).

2.  Действительные токи ветвей I1, I2, I3 и их направления также показаны на (рис 2.3).

3.  связь действительных и контурных токов:

I1=I11; I2=I22—I11; I3=I22

4.  Составим систему уравнений для контурных токов по второму закону Кирхгофа:

 

E1 — E2 = I11·(R1 + R5 + R2) — I22·R2

E2 = I22·(R2 + R4 + R3) — I11·R2;

5-15=11·I11-5·I22

15=11·I22-5·I11.

Решив систему уравнений получим:

I11= -0,365

I22= 1,197, тогда

I1= -0,365; I2= 1,562; I3= 1,197

Как видим реальные значения токов ветвей совпадают с полученными значениями в примере 2.

2.4 Метод узлового напряжения (метод двух узлов).

Часто встречаются схемы содержащие всего два узла; на рис. 2.4 изображена одна из таких схем.

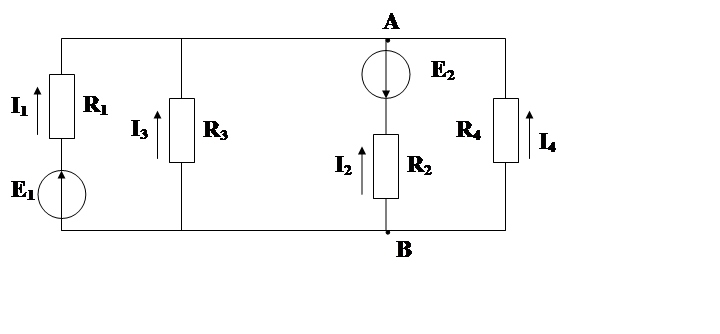
Рис 2.4. К расчету электрических цепей методом двух узлов.

Наиболее рациональным методом расчета токов в них является Метод двух узлов.

Под Методом двух узлов понимают метод расчета электрических цепей, в котором за искомое напряжение ( с его помощью затем определяют токи ветвей) принимают напряжение между двумя узлами А и В схемы – UАВ.

Напряжение UАВ может быть найдено из формулы:

UАВ=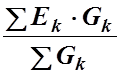

В числителе формулы знак «+», для ветви содержащей ЭДС, берется если направление ЭДС этой ветви направлено в сторону повышения потенциала, и знак «-» если в сторону понижения. В нашем случае, если потенциал узла А принять выше потенциала узла В (потенциал узла В принять равным нулю), Е1 G1, берется со знаком «+», а Е2·G2 со знаком «-»:

UАВ=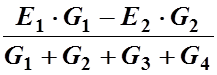

Где G – проводимости ветвей.

Определив узловое напряжение, можно вычислить токи в каждой ветви электрической цепи:

IК=(Ек-UАВ)GК.

Если ток имеет отрицательное значение, то действительное его направление является противоположным обозначенным на схеме.

В этой формуле, для первой ветви, т. к. ток I1 совпадает с направлением Е1, то ее значение принимается со знаком плюс, а UАВ со знаком минус, т. к. направлено навстречу току. Во второй ветви и Е2 и UАВ направлены навстречу току и берутся со знаком минус.

Пример 4. Для схемы рис. 2.4 если Е1= 120В, Е2=5Ом, R1=2Ом, R2=1Ом, R3=4Ом, R4=10Ом.

UАВ=(120·0,5-50·1)/(0,5+1+0,25+0,1)=5,4 В

I1=(E1-UАВ)·G1= (120-5,4)·0,5=57,3А;

I2=(-E2-UАВ)·G2 = (-50-5,4)·1 = -55,4А;

I3=(О-UАВ)·G3 = -5,4·0,25 = -1,35А;

I4=(О-UАВ)·G4 = -5,4·0,1 = -0,54А.

2.5. Нелинейные цепи постоянного тока и их расчет.

До сих пор мы рассматривали электрические цепи, параметры которых (сопротивления и проводимости) считались не зависящими от величины и направления проходящего по ним тока или приложенного к ним напряжения.

В практических условиях большинство встречающихся элементов имеют параметры зависящие от тока или напряжения, вольт-амперная характеристика таких элементов имеет нелинейный характер (рис. 2.5),такие элементы называются Нелинейными. Нелинейные элементы широко используются в различных областях техники (автоматики, вычислительной техники и других).

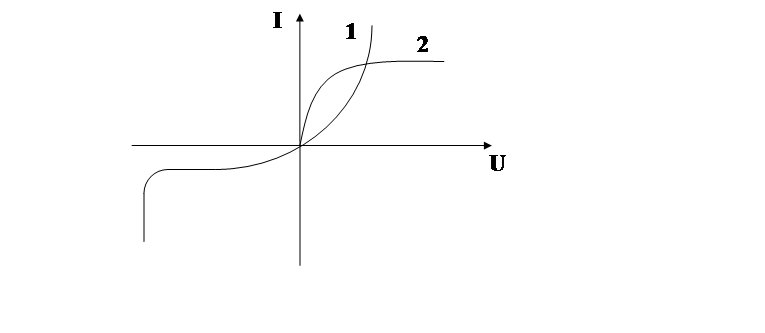
Рис. 2.5. Вольт-амперные характеристики нелинейных элементов:

1 — полупроводникового элемента;

2 — термосопротивления

Нелинейные элементы позволяют реализовать процессы которые невозможны в линейных цепях. Например, стабилизировать напряжение, усиливать ток и другие.

Нелинейные элементы бывают управляемыми и неуправляемыми. Неуправляемые нелинейные элементы работают без влияния управляющего воздействия (полупроводниковые диоды, термосопротивления и другие). Управляемые элементы работают под влиянием управляющего воздействия (тиристоры, транзисторы и другие). Неуправляемые нелинейные элементы имеют одну вольт-амперную характеристику; управляемые – семейство характеристик.

Расчет электрических цепей постоянного тока чаще всего производят графическими методами, которые применимы при любом виде вольт-амперных характеристик.

Последовательное соединение нелинейных элементов.

На рис. 2.6 приведена схема последовательного соединения двух нелинейных элементов, а на рис. 2.7 их вольтамперные характеристики – I(U1) и I(U2)

R1(I)

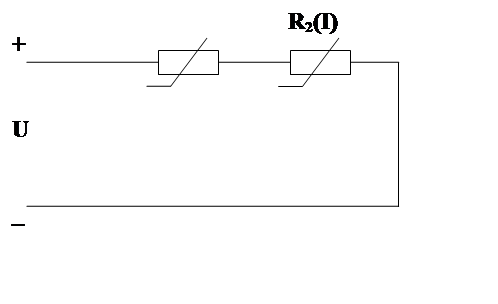
Рис. 2.6 Схема последовательного соединения

Нелинейных элементов.

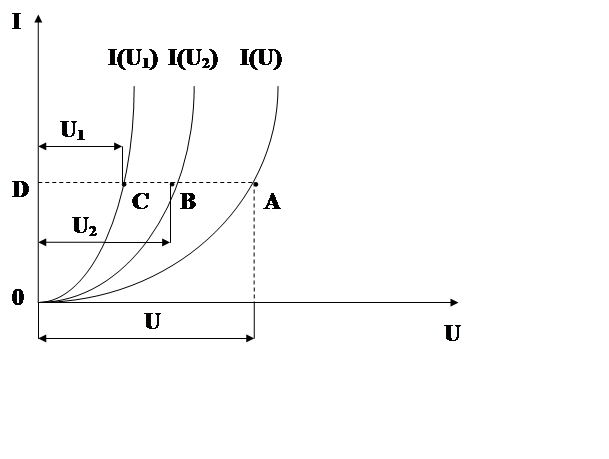
Рис. 2.7 Вольтамперные характеристики нелинейных элементов.

Построим вольт-амперную характеристику I(U), выражающую зависимость тока I в цепи от приложенного к ней напряжения U. Так как ток обоих участков цепи одинаков, а сумма напряжений на элементах равна приложенному (рис. 2.6) U=U1+U2, то для построения характеристики I(U) достаточно просуммировать абсциссы заданных кривых I(U1) и I(U2) для определенных значений тока. Пользуясь характеристиками (рис. 2.6) можно решить различные для этой цепи задачи. Пусть, например, задана величина приложенного к току напряжения U и требуется определить ток в цепи и распределение напряжений на ее участках. Тогда на характеристике I(U) отмечаем точку А соответствующую приложенному напряжению U и проводим от нее горизонталь пересекающую кривые I(U1) и I(U2) до пересечения с осью ординат (точка D), которая показывает величину тока в цепи, а отрезки ВD и СD величину напряжения на элементах цепи. И наоборот по заданному току можно определить напряжения как общее, так и на элементах.

Параллельное соединения нелинейных элементов.

При параллельном соединении двух нелинейных элементов (рис. 2.8) с заданными вольт-амперными характеристиками в виде кривых I1(U) и I2(U) (рис. 2.9) напряжение U является общим, а ток I в неразветвленной части цепи равен сумме токов ветвей:

I = I1 + I2

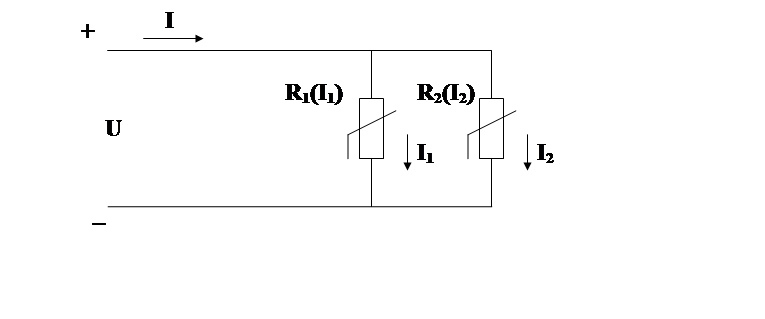
Рис. 2.8 Схема параллельного соединения нелинейных элементов.

Поэтому для получения общей характеристики I(U) достаточно для произвольных значений напряжения U на рис. 2.9 просуммировать ординаты характеристик отдельных элементов.

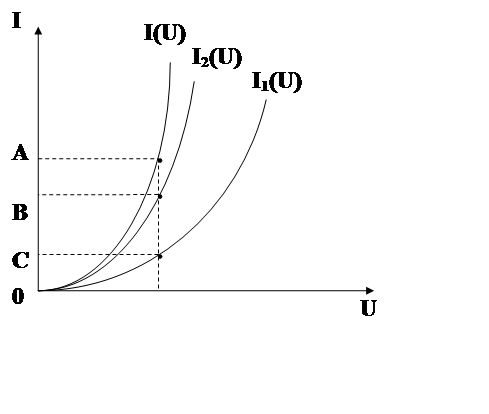
Рис. 2.9 Вольт-амперные характеристики нелинейных элементов.