Энергия магнитного поля катушки
При изучении явления электромагнитной индукции рассматривалась ЭДС индукции, возникающая в контуре в результате изменения потока магнитной индукции через площадку, ограниченную контуром, когда магнитное поле создается внешними источниками (магнитами или проводниками с током). Но последовательный подход предполагает, что это явление не зависит от природы магнитного поля и от характера источников, создающих его. В частности, магнитное поле создается не только внешними источниками, но и током в самом рассматриваемом контуре.
Магнитное поле этого тока в любой точке пространства пропорционально протекающему току: Bi ~ I, хотя и зависит от положения выбранной точки относительно проводника. Следовательно, магнитный поток этого вектора через элементарную поверхность DSi в точке наблюдения также пропорционален току:
![]()
Отсюда сразу же следует вывод, что поток магнитной индукции через поверхность, «натянутую» на рассматриваемый контур, оказывается пропорционален силе протекающего тока:
![]()
Таким образом, ток, протекающий в любом контуре, создает магнитный поток через него, который определяется выражением:
Ф = LI.
Коэффициент пропорциональности L, зависящий от размеров контура и расположения проводника, его ограничивающего, называется Индуктивностью.
Единица индуктивности – генри (Гн). При индуктивности 1 Гн и силе тока 1 А ток в проводнике создает магнитный поток, равный 1 Тл.
Индуктивность любого контура – положительная величина. Можно показать, что индуктивность контура увеличивается в 2 раза, когда все линейные размеры контура увеличиваются вдвое.
Индуктивность катушки пропорциональна квадрату числа витков:
LN = N 2L1,
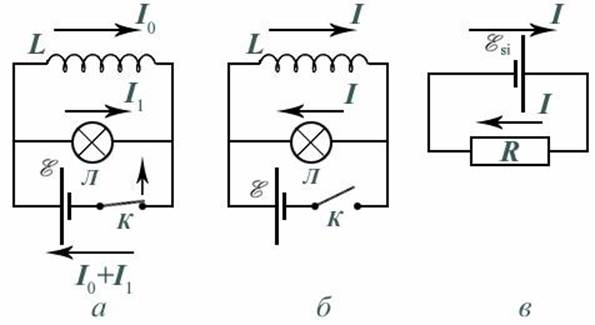
Рис. 1
Где L1 – индуктивность одного витка. Так как намотать катушку, содержащую 1000 витков провода, достаточно легко, то ясно, что индуктивность катушки легко изменить, сделав ее в миллион раз больше, чем индуктивность одного витка. На принципиальных электрических схемах элемент с большой индуктивностью изображается в виде нескольких витков (рис. 1).
Для наблюдения явления самоиндукции можно использовать электрическую схему, содержащую источник тока, лампу накаливания и катушку с током (см. рис. 1,а). При замкнутом ключе по катушке L течет ток I0, а по лампе Л – ток I1, и лампочка светится. После размыкания ключа лампа гаснет не сразу, а если I0 > I1, то в первый момент она ярко вспыхивает (рис. 1,б). В контуре из катушки и лампочки течет ток I благодаря тому, что уменьшение силы тока в катушке индуктивности от начального значения I0 до нуля, приводит к уменьшению магнитного потока и возникновению ЭДС самоиндукции:
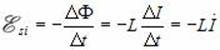
Сила тока будет уменьшаться гораздо медленнее, чем в отсутствие катушки. При сопротивлении проводов катушки, малом по сравнению с сопротивлением нити накала лампы, сила тока определяется уравнением
![]() Si = RI,
Si = RI,
Или
![]()
Где R – сопротивление нити накала лампы Л (рис. 1,в).
Можно показать, что в этом случае сила тока должна уменьшаться во времени по следующему закону:
![]()
При этом на резисторе за время прохождения тока в соответствии с законом Джоуля–Ленца выделится количество теплоты, равное:
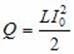
Этот факт можно истолковать так, что катушка индуктивностью L, по которой течет ток I, обладает энергией, равной:
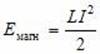
И связанной с тем, что в катушке существует магнитное поле.