Значення нарисної геометрії, як теорії зображень та її роль у формуванні просторового інженерного мислення. Короткий історичний огляд. Геометричні фігури. Геометричний простір. Відображення. Метод проекціювання. Центральне та паралельне проекціювання. Основні властивості
1.1. Предмет нарисної геометрії, як частина інженерної графіки. Зображення як геометрична модель простору
Інженерна графіка — це дисципліна, яка складається з двох дисциплін: нарисної геометрії та технічного креслення.
Нарисна геометрія є розділом геометрії, в якому вивчають способи подання просторових фігур або оригіналів за допомогою їхніх зображень (графічних моделей) на площині чи на поверхні.
Предметом нарисної геометрії є розробка методів побудови та читання креслень, способів розв’язування за допомогою креслень геометричних задач, методів геометричного моделювання, тобто створення проекцій об’єкта, який відповідав би наперед заданим геометричним та іншим вимогам, а також побудова зображень предметів та об’єктів деякої конкретної галузі інженерної діяльності. Для розв’язування інженерних задач методами геометричного моделювання в різних галузях науки й техніки методи нарисної геометрії мають бути доповнені методами обчислювальної геометрії, що лежить в основі комп’ютерної графіки. У свою чергу, методи обчислювальної геометрії грунтуються на досягненні окремих математичних наук.
Комп ‘ютерна графіка — це сукупність технічних, програмних, мовних засобів і методів зв’язку користувача з ЕОМ на рівні зорових образів при розв’язуванні різних задач.
Для відтворення форми, розмірів об’єктів та положення їх у просторі з метою створення оригіналу за його проекціями застосовують геометричні моделі. При цьому велику роль відіграє теорія параметризації, яка розглядає задання форми та положення геометричної фігури за допомогою набору даних або умов.
Новітні сучасні технології передбачають знання багатьох нових питань, методів та задач, зокрема застосування складних кривих поверхонь. Це сприяло вивченню та конструюванню цих поверхонь каркасно-параметричним, каркасно-кінематичним та іншими методами, в яких додатково використовується апарат аналітичної та диференціальної геометрії.
Комп’ютеризація різних галузей народного господарства, широке використання електронно-обчислювальної техніки, дисплеїв та графопобудовників показали принципіальну можливість виконання графічних зображень за допомогою персональних комп’ютерів.
Зараз уже стало очевидним, що комп’ютерна графіка може розвиватися на основі широкого використання законів та правил нарисної геометрії, інженерної графіки та обчислювальної геометрії.
1.2. Короткий історичний огляд
Перші рисунки, близькі до сучасних прямокутних проекцій, трапляються вже на стінах давніх храмів і палаців Єгипту та Ассирії. За’часів Стародавньої Греції та Риму для побудови зображень також використовувалися прямокутні та центральні проекції на одну площину. Зодчі Київської
Русі створили такі всесвітньо відомі пам’ятки архітектури, як Софію Київську, Золоті Ворота, які й зараз викликають захоплення. Правила будівництва були викладені в "Будівельному статуті" та в Руській Правді (1020 р.) Ярослава Мудрого. Там же були наведені зображення, побудовані за проекційним принципом.
Новий період розвитку нарисної геометрії починається в епоху Ренесансу, коли з розквітом архітектури та живопису особливого значення набуває перспектива.
У Росії плани Пскова (XV ст.) та Москви (XVII ст.) свідчать про те, що вже тоді було уявлення не тільки про способи виконання фасадів та планів, а й про аксонометрію.
Креслень зодчих Київської Русі не збереглося, хоч є підстави вважати, що майстри користувалися схематичними рисунками. Винятковий інтерес становить креслення будови, виконане гострим предметом налесо-вому грунті біля Десятинної церкви в Києві.
Окремі види проекцій використовувалися в техніці до кінця XVIII ст., коли в 1799 р. з’явилася знаменита "Оеотеїгіе (іексгірііуе" Гаспара Монжа (1746—1818). У цій геометрії окремі прямокутні проекції на вертикальні та горизонтальні площини були зведені в єдину систему. В Росії перший курс нарисної геометрії був прочитаний у 1810 р. в інституті (корпусі) інженерів шляхів сполучення учнем Монжа інженером К. І. Потье. В 1821 р. вийшов перший російський підручник з нарисної геометрії Я. О. Сева-стьянова (1796—1849). У ньому було вміщено велику кількість задач прикладного характеру. Схему курсу Я. О. Севастьянова використав М. І. Макаров (1824—1904), а вдосконалив її В. І. Курдюмов (1853— 1904). Послідовниками цього курсу були професори М. О. Ринін (1877—1942) та О. І. Добряков (1895—1947).
Новий етап розвитку нарисної геометрії та інженерної графіки почався в 40-ві роки XX ст., коли в Москві професор М. Ф. Чет-верухін (1891—1974), а в Києві професор С. М. Колотов (1880—1965) опублікували ряд наукових праць, які започаткували систематичні наукові та науково-методичні дослідження в цій галузі знань.
Професор 1.1. Котов (1909—1976) перший застосував апарат нарисної геометрії до розв’язування прикладних задач у різних галузях техніки. Він розробив також основні принципи застосування ЕОМ у курсі нарисної геометрії, заснувавши московський семінар "Кібернетика графіки". У результаті діяльності цього семінару, а також завдяки активній праці передових кафедр України та Росії усталився етап розвитку нарисної геометрії, який можна назвати етапом геометричного моделювання, або інженерної геометрії, коли за наперед заданими умовами та вимогами формуються оптимальні геометричні моделі майбутнього виробу.
1.3. Геометричні фігури. Геометричний простір. Відображення
Довільну множину точок називають геометричною фігурою. Геометричних фігур дуже багато, але основними є три: точка, пряма, площина. Між основними фігурами існують різні співвідношення, які можна визначити словами: належати, бути паралельними, міститися "між", бути конгруентними. Три співвідношення характеризують позиційні властивості геометричних фігур, а вираз "бути конгруентним" означає метричну властивість.
Позиційна властивість визначає розміщення геометричних фігур на площині та в просторі на основі взаємної належності (інцидентності) одних фігур до інших або якщо такої належності немає. Належність може бути повною (наприклад, пряма лежить у площині), частковою (пряма перетинається з площиною в точці) або її може не бути взагалі (дві мимобіжні прямі).
Метричні властивості пов’язуються з визначенням метричних характеристик (розмірів) відстаней, кутів та площ.
Залежно від характеру властивостей розрізняють позиційні та метричні задачі.
Основою нарисної геометрії є метод проекцій, який дає змогу діставати зображення просторових фігур на площині чи поверхні. Якщо взяти в просторі довільну точку 8 і сполучити її прямими з іншими точками простору, то дістанемо в’язку прямих. Точку 8 називають центром. Якщо центр задано, то через нього та кожну точку простору можна провести єдину пряму, яку називають проекціювальним променем. Перетин проекціювального променя з площиною проекцій дає проекцію точки.
1.4. Метод проекціювання. Центральне та паралельне проекціювання. Основні властивості
Для центрального та паралельного проекціювання характерна прямолінійність проекціювальних ліній, які у своїй сукупності утворюють в’язки. Центр в’язки — точка S може бути власною (при центральному проекціюванні) та невласною (при паралельному проекціюванні).
Якщо в просторі визначити об’єкт проекціювання, наприклад кілька точок, задати центр проекціювання S’та площину проекцій, то проекціями заданих точок є точки перетину проекціювальних променів, що проходять через відповідні точки, з площиною проекцій (рис. 1.1, а… в). При невласному центрі проекціювання, заданому напрямом З", проекціювальні промені паралельні між собою, а з площиною проекцій вони можуть утворювати гострі чи прямі кути. Залежно від цього розрізняють косокутне та прямокутне проекціювання.
За способом проекціювання проекції називають центральними, косокутними чи прямокутними. Ці проекції характеризуються певними властивостями.
Проекцією прямої в загальному випадку є пряма, що проходить через точку її перетину з площиною проекцій. Якщо задано проекції хоча б двох точок прямої, то можна визначити проекцію всієї прямої
(рис. 1.2, а). Якщо пряма паралельна площині, то її центральна та паралельна проекції паралельні цій прямій (рис. 1.2, б).
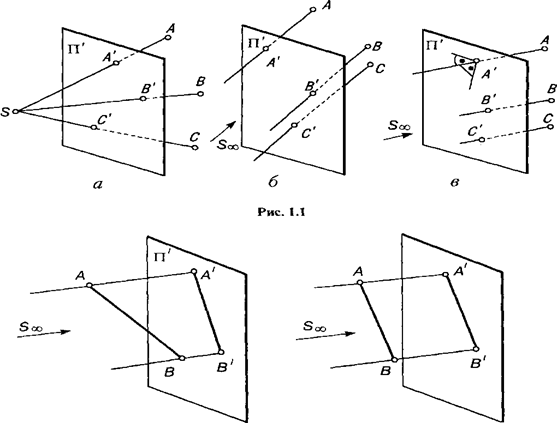
Рис.1.2
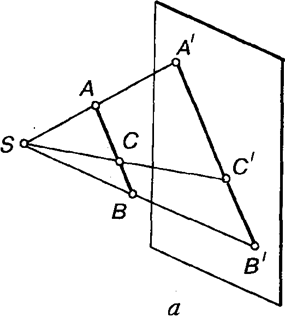
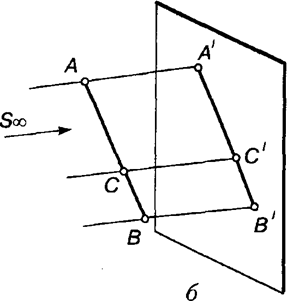
Рис.1.3
Якщо на відрізку прямої, паралельної площині проекцій, задати точку, що лежить між даними точками, то проекції утворених відрізків при центральному проек-ціюванні будуть пропорційні до заданих (рис. 1.3, а), а при паралельному — дорівнюватимуть їм (рис. 1.3, б).
Згідно з рис. 1.3 при паралельному про-екціюванні відношення довжин відрізків прямої та їхніх проекцій зберігається:
АВ =А’В’
ВС В’С.
Це відношення називають простіш відношенням трьох точок. Воно є інваріантом (незмінною властивістю) паралельного про-екціювання. Отже, при паралельному проекціюванні відношення проекцій відрізків паралельних прямих заданого напряму до дійсних довжин відрізків є сталою величиною. Цю величину називають коефіцієнтом спотворення відрізків заданого напряму.
Список рекомендованої літератури
Гордон В. О., Семенцов-Огиевский М. А. Курс начертательной геометрии.- М.: Изд-во Наука, 1988. – 270 с.
Михайленко В. Є., Ковальов С. М. та ін. Нарисна геометрія. Підручник для вузів. – К.:Вища школа,1993. – 134с.
Винницкий И. Г. Начертательная геометрия. Учебник для вузов. – М.: Высшая школа, 1985.- 168с.
Михайленко В. Е. та ін. Инженерная графика. – Киев: Высшая школа, 1990.-290 с.
Михайленко В. Е. та ін. Інженерна та комп’ютерна графіка. За ред. Михайленка В. Е. Київ: Вища школа, 2000.