Цель: Научиться проводить линии регрессии различных типов, сглаживать данные и прогнозировать значения временных рядов, используя методы математического анализа и средства, предоставляемые Excel.
План занятия:
Решить задачу об управлении портфелем акций, используя методику, приведенную ниже.
Самостоятельно решить задачу об отыскании момента продажи акций.
Решить задачу об определении параметров регрессионной кривой.
Порядок выполнения работы
Решим задачу об определении момента продажи или покупки пакета акций с помощью прогнозирования динамики цены на ценные бумаги.
Запустите Excel и на первом листе создайте следующую таблицу:
|
Номер |
Дата |
Курс акций |
|
1 |
01.01.00 |
5,42 |
|
2 |
02.01.00 |
5,12 |
|
3 |
03.01.00 |
4,42 |
|
4 |
04.01.00 |
4,19 |
|
5 |
05.01.00 |
3,79 |
|
6 |
06.01.00 |
3,20 |
|
7 |
07.01.00 |
2,54 |
|
8 |
08.01.00 |
2,22 |
|
9 |
09.01.00 |
1,97 |
|
10 |
10.01.00 |
1,83 |
|
11 |
11.01.00 |
1,66 |
|
12 |
12.01.00 |
1,10 |
|
13 |
13.01.00 |
0,99 |
|
14 |
14.01.00 |
0,94 |
|
15 |
15.01.00 |
0,86 |
|
16 |
16.01.00 |
0,73 |
|
17 |
17.01.00 |
0,62 |
|
18 |
18.01.00 |
0,60 |
Постройте по этой таблице точечный график (номер – курс акций) и оформите его на свой вкус.
Для определения среднего хода изменения цены проведем линию регрессии. Для этого необходимо на любой точке данных на графике щелкнуть правой кнопкой мыши и в открывшемся контекстном меню выбрать пункт "Добавить линию тренда".
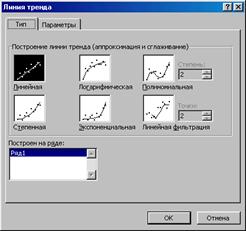 Открывшееся окно позволяет выбрать один из возможных типов линии тренда:
Открывшееся окно позволяет выбрать один из возможных типов линии тренда:
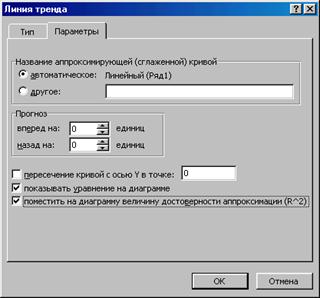
Вкладка "Параметры" позволяет задать значения для экстраполяции (прогноза) и другие параметры. Нас будет интересовать уравнение проводимой линии и величина достоверности аппроксимации. Включите соответствующие опции на вкладке "Параметры", как показано ниже:
Дальнейшая задача: подобрать линию тренда, которая наилучшим образом описывает данный временной ряд. Критерием будет являться величина достоверности аппроксимации. Строя линии тренда различных типов и занося в отдельную таблицу значения R, выберите ту из них, у которой R – наибольшее.
 Результаты заносите в таблицу:
Результаты заносите в таблицу:
|
Вид линии тренда |
R |
Так как для линейной фильтрации уравнение не предусмотрено, то ее не следует принимать во внимание. Для полиномиальной линии следует ограничиваться полиномом до 4-ой степени, иначе линия начинает в значительной степени повторять случайные колебания цен.
Постройте на диаграмме выбранную вами линию тренда. Для экстраполяции за пределы наблюдаемых данных щелкните на ней правой кнопкой мыши и в открывшемся контекстном меню выберите пункт: "Формат линии тренда". Установите прогноз на несколько периодов вперед, чтобы определить приблизительный момент экстремума.
Для определения точного момента экстремума следует выписать уравнение линии тренда, взять производную, приравнять ее к нулю и найти, таким образом, момент минимальной цены, когда, собственно, и следует покупать пакет акций.
Покажите результаты вычислений и график преподавателю.
Проведите самостоятельно аналогичные расчеты для следующего временного ряда:
|
Номер |
Цена |
Курс акций |
|
1 |
01.01.00 |
1,00 |
|
2 |
02.01.00 |
2,00 |
|
3 |
03.01.00 |
3,00 |
|
4 |
04.01.00 |
6,00 |
|
5 |
05.01.00 |
7,00 |
|
6 |
06.01.00 |
9,00 |
|
7 |
07.01.00 |
11,00 |
|
8 |
08.01.00 |
10,00 |
|
9 |
09.01.00 |
13,97 |
|
10 |
10.01.00 |
18,00 |
|
11 |
11.01.00 |
20,00 |
|
12 |
12.01.00 |
19,73 |
|
13 |
13.01.00 |
20,00 |
|
14 |
14.01.00 |
24,00 |
|
15 |
15.01.00 |
26,00 |
|
16 |
16.01.00 |
25,00 |
|
17 |
17.01.00 |
26,00 |
|
18 |
18.01.00 |
28,00 |
|
19 |
19.01.00 |
28,00 |
|
20 |
20.01.00 |
30,00 |
7. Построим линию тренда, используя формулы линейной регрессии:
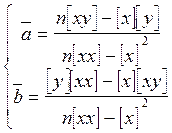
Где: 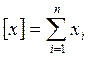 ;
; 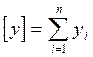 ;
; 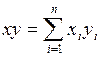 ;
; 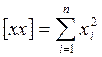 и т. д.
и т. д.
Наберите на листе 3 таблицу с исходными данными (начиная с ячейки А1):
|
X |
Y |
|
1 |
-7 |
|
2 |
-3 |
|
3 |
-3 |
|
4 |
0 |
|
5 |
0 |
|
6 |
7 |
|
7 |
8 |
|
8 |
9 |
|
9 |
10 |
|
10 |
14 |
|
11 |
15 |
|
12 |
21 |
|
13 |
24 |
|
14 |
28 |
|
15 |
24 |
|
16 |
30 |
|
17 |
35 |
|
18 |
34 |
|
19 |
40 |
|
20 |
45 |
В колонке С вычислите значения Х2. В колонку D добавьте заголовки для формул:
|
А |
B |
C |
D |
E |
|
X |
Y |
Х^2 |
Сумма Х |
|
|
1 |
-7 |
Сумма Y |
||
|
2 |
-3 |
Сумма XY |
||
|
3 |
-3 |
Сумма ХХ |
||
|
4 |
0 |
Сумма Х^2 |
||
|
5 |
0 |
N= |
||
|
6 |
7 |
|||
|
7 |
8 |
A= |
||
|
8 |
9 |
B= |
||
|
9 |
10 |
Наклон= |
||
|
10 |
14 |
Отрезок= |
||
|
11 |
15 |
|||
|
12 |
21 |
|||
|
13 |
24 |
|||
|
14 |
28 |
|||
|
15 |
24 |
|||
|
16 |
30 |
|||
|
17 |
35 |
|||
|
18 |
34 |
|||
|
19 |
40 |
|||
|
20 |
45 |
Занесите в ячейки Е1 … Е10 формулы для расчета параметров линии тренда:
Е1: сумма значение Х;
Е2: сумма значений Y;
Е3: сумму призведений XY (функция СУММПРОИЗВ);
Е4: сумма значений Х2 (из колонки С);
Е5: сумму Х, возведенную в квадрат (квадрат ячейки Е1);
Е6: общее число точек (20 штук);
Е8: формулу для значения коэффициента а (см. формулу выше);
Е9: формулу для значения коэффициента b (см. формулу выше);
Для проверки используем функции, позволяющие без промежуточных вычислений получить эти коэффициенты (они вызываются через мастер функций и находятся в группе статистических функций):
Е10: используем функцию НАКЛОН;
Е11: используем функцию ОТРЕЗОК.
Постройте точечный график по экспериментальным точкам и проведите по нему линейную регрессию с выводом уравнения на диаграмму. Сравните полученные разными способами значения коэффициентов регрессии. Покажите результат преподавателю.
Контрольные вопросы.
Какие типы линий тренда поддерживает Excel?
Как подбирается линия тренда для предлагаемой задачи?
Как определить коэффициенты уравнения линии тренда?
Как найти момент экстремума для полученной кривой?
Какие функции служат для определения коэффициентов линейной регрессии?
Как построить прогноз значений, используя линию тренда?